Question 4
Statement-1: A force of constant magnitude can cause variable acceleration of a particle.
Statement-2: A force of constant magnitude can cause only constant acceleration.
Statement-1is true,Statement-2is true
Statement-1is false,Statement-2is true
Statement-1is true,Statement-2is false
Statement-1is false,Statement-2is false

Video Solution

Answer

Step by step video & image solution for Question 4 Statement-1: A force of constant magnitude can cause variable acceleration of a particle. Statement-2: A force of constant magnitude can cause only constant acceleration. Statement-1is true,Statement-2is true Statement-1is false,Statement-2is true Statement-1is true,Statement-2is false Statement-1is false,Statement-2is false by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Similar Questions

Let R be the set of real numbers. Statement-1 : $A = {(x, y) \in R \times R : y - x$ is an integer} is an equivalence relation on R. Statement-2 : $B = {(x, y) \in R \times R : x = α y$ for some rational number a} is an equivalence relation on R.
Statement-1 is true, Statement-2 is true. Statement-2 is a correct explanation for Statement-1.
Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
Statement-1 is true, Statement-2 is false.
Statement-1 is false, Statement-2 is true.
View Solution
Let A and B be two symmetric matrices of order 3. Statement-1 : A(BA) and (AB)A are symmetric matrices. Statement-2 : AB is symmetric matrix if matrix multiplication of A with B is commutative. Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1. Statement-1 is true, Statement-2 is true; Statement-2 is true; Statement-2 is not a correct explanation for Statement-1. Statement-1 is true, Statement-2 is false. Statement-1 is false, Statement-2 is true.
View Solution
a. Statement- 1 and Statement- 2 are true, and state-ment- 2 is the correct explanation of Statement- 1.
b. Statement- 1 and Statement- 2 are true but Statement- 2 is not the correct explanation of Statement- 1.
c. Statement- 1 is true and Statement- 2 is false.
d. Statement- 1 is false and Statement- 2 is true.
e. Statement- 1 is false and Statement- 2 is false.
Statement- 1:
Compound (I) is formed not (II).
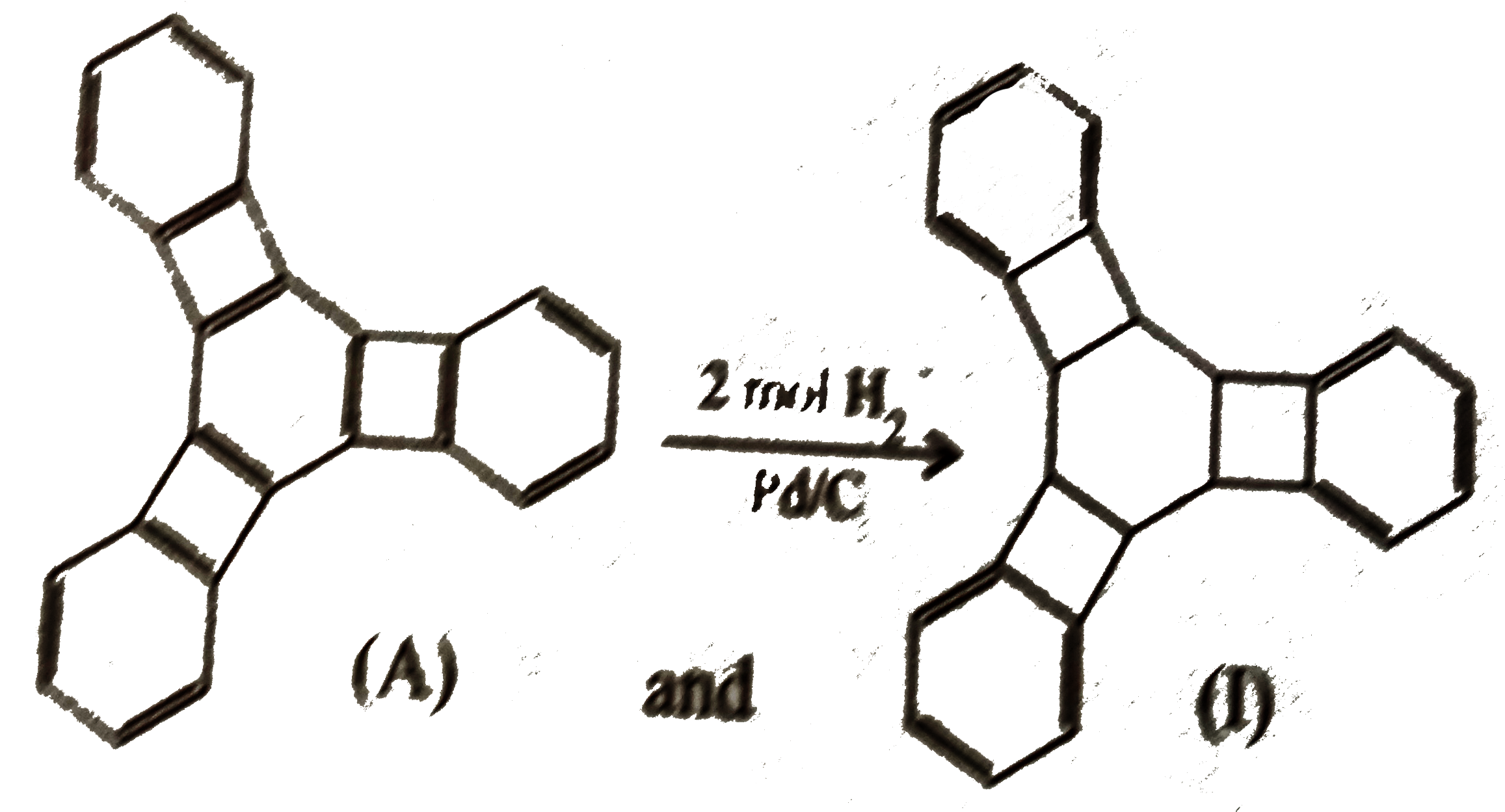and
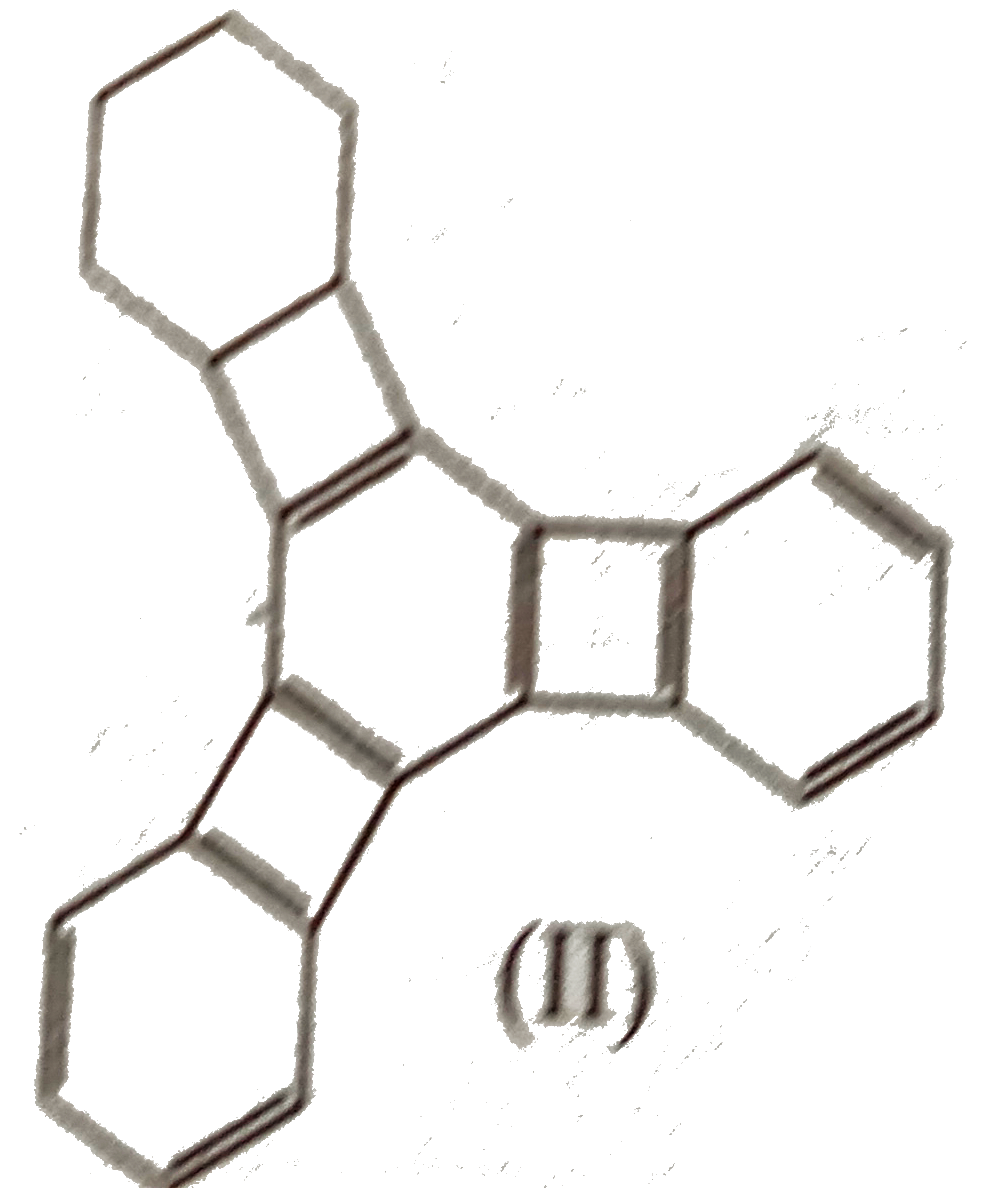
Statement- 2:
Due to the reduction of central ring, 3 four-membered anti-aromatic rings become stable to from (I). In (II), due to the reduction of terminal ring, only one anti-aromatic ring can be stabilised.
View Solution
Statement -1 ${(\frac{1}{2})}^{7} < {(\frac{1}{3})}^{4}$
$\Rightarrow 7 log (\frac{1}{2}) < 4 log (\frac{1}{3}) \Rightarrow 7 < 4$
Statement-2 If $a x < a y$ , where $a < 0$ ,x, $y > 0$ , then $x > y$ .
(a) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1
Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -1
(c) Statement -1 is true, Statement -2 is false
(d) Statement -1 is false, Statement -2 is true.
View Solution
Statement-1(Assertion) and Statement-2 (reason) Each of these question also has four alternative choices, only one of which is the correct answer. You have to select the correct choice as given below.
(a) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1
Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -1
(c) Statement -1 is true, Statement -2 is false
(d) Statement -1 is false, Statement -2 is true
Statement -1 The equation ${(log x)}^{2} + {log x}^{2} - 3 = 0$ has two distinct solutions.
Statement-2 ${log x}^{2}$ =2logx.
View Solution
Statement-1(Assertion) and Statement-2 (reason) Each of these question also has four alternative choices, only one of which is the correct answer. You have to select the correct choice as given below.
(a) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1
Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -1
(c) Statement -1 is true, Statement -2 is false
(d) Statement -1 is false, Statement -2 is true
Statement -1 ${log}_{x} 3 . {log}_{x / 9} 3 = {log}_{81} (3)$ has a solution.
Statement-2 Change of base in logarithms is possible .
View Solution
Let $f (x) = {x^{n} sin (\frac{1}{x}), x \neq 0; 0, x = 0$ ; and $n > 0$ Statement-1: $f (x)$ is continuous at $x = 0$ and $\forall n > 0$ . and Statement-2: $f (x)$ is differentiable at $x = 0$ $\forall n > 0$ (1) Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1. (2) Statement-1 is True, Statement-2 is True Statement-2 is NOT a correct explanation for Statement-1. (3) Statement-1 is True, Statement-2 is False (4) Statement-1 is False, Statement-2 is True.
View Solution
Statement-1 : The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is $^9 C_{3}$ . Statement-2 : The number of ways of choosing any 3 places from 9 different places is $^9 C_{3}$ . Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1. Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1. Statement-1 is true, Statement-2 is false. Statement-1 is false, Statement-2 is true.
View Solution
Statement-1(Assertion) and Statement-2 (reason) Each of these question also has four alternative choices, only one of which is the correct answer. You have to select the correct choice as given below.
(a) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1
Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -1
(c) Statement -1 is true, Statement -2 is false
(d) Statement -1 is false, Statement -2 is true
Statement -1 The equation $7^{{log}_{7} (x^{3} + 1)} - x^{2} = 1$ has two distinct real roots .
Statement -2 $a^{{log}_{a} N} = N$ , where $a > 0$ , $a \neq 1$ and $N > 0$
View Solution
Statement-1(Assertion) and Statement-2 (reason) Each of these question also has four alternative choices, only one of which is the correct answer. You have to select the correct choice as given below.
(a) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1
Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -1
(c) Statement -1 is true, Statement -2 is false
(d) Statement -1 is false, Statement -2 is true
Statement -1 The equation $x^{{log}_{x} {(1 - x)}^{2}} = 9$ has two distinct real solutions.
Statement -2 $a^{{log}_{a} b} = b$ , when $a < 0, a \neq 1, b > 0$ .
View Solution

Similar Questions

Recommended Questions