Let . The locus of all points for which the line OP (where O is the origin ) cuts the line in Q such that PQ =d is
A
B
C
D
Video Solution
Text Solution
The correct Answer is:B
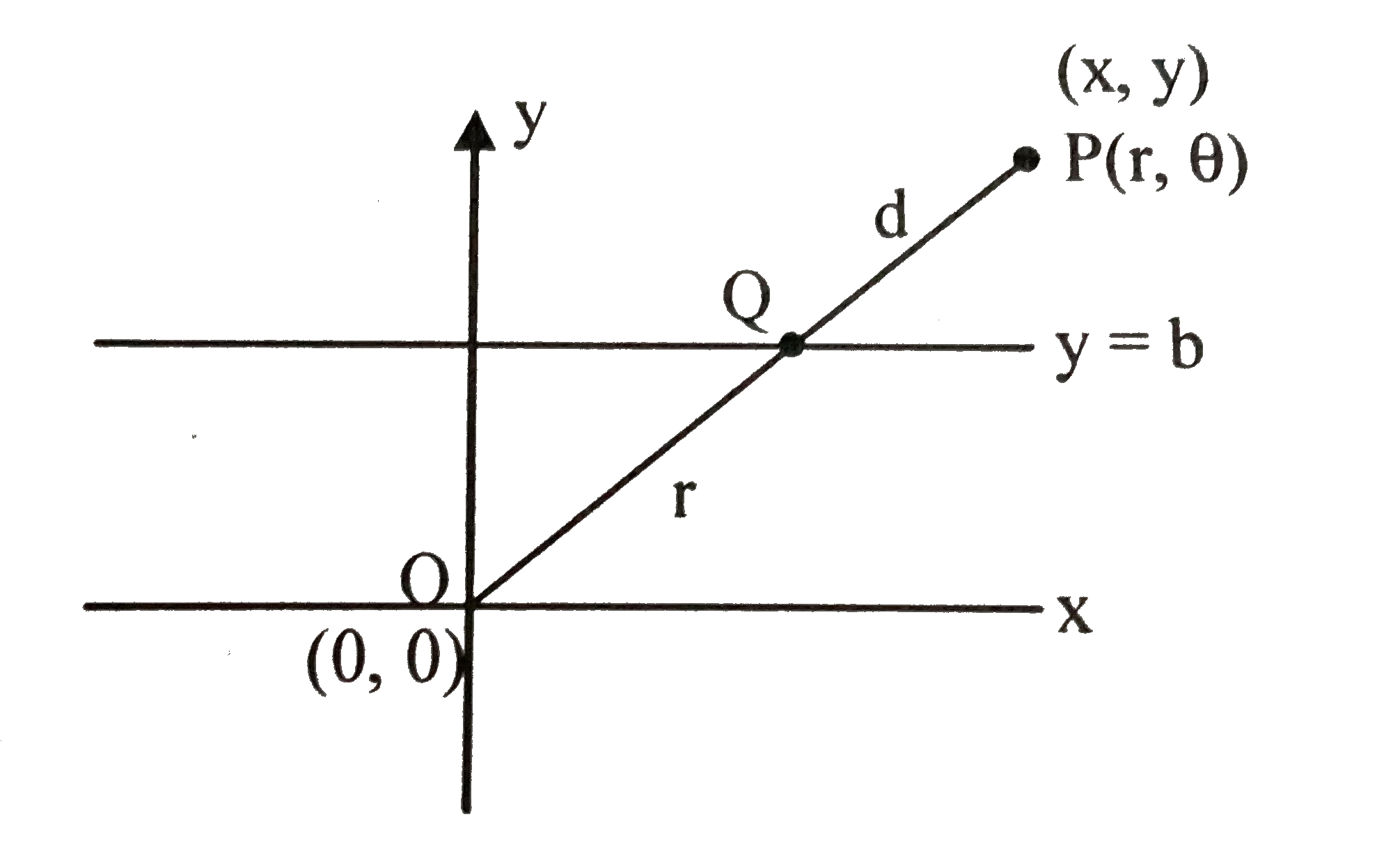
equation of OP
point Q is
points P is
|
Topper's Solved these Questions
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:PART-II MATHEMATICS
Explore 10 Videos
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:Part A - Mathematics
Explore 20 Videos
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:PART-2(MATHEMATICS)
Explore 10 Videos
- KVPY 2021Book:KVPY PREVIOUS YEARChapter:KVPY 2021Exercise:PART II MATHEMATICS
Explore 4 Videos
Similar Questions
Knowledge Check
The locus of a point P which divides the line joining (1, 0) and (2cosθ,sinθ) internally in the ratio 2 : 3 for all θ is
Aa straight lineBa circleCa pair of straight linesDa parabolaThe locus of a point P which divides the line joining (1, 0) and (2cosθ,2sinθ) internally in the ratio 2:3 for all θ, is a
Astraight lineBcircleCpair of straight lineDparabolaThe locus of the points of intersection of the lines xcosθ+ysinθ=a and xsinθ−ycosθ=b, (θ= variable) is :
Ax2+y2=a2+b2Bx2+y2=a2−b2Cx2+y2=2(a2+b2)DNone of the above
The locus of a point P which divides the line joining (1,0)and(2cosθ,2sinθ) intermally in the ratio 1:2 for all θ. is
View SolutionThe co-ordinate of the point P are (x, y, z) and the direction cosines of the line OP when O is the origin are l, m, n. If OP = r, then
View SolutionLet A be the set of all points in a plane and let O be the origin Let
R={(p,q):OP=OQ}. then ,R is
View SolutionLet A be the set of all points in a plane and let O be the origin Let
R={(p,q):OP=OQ}. then ,R is
View SolutionLet A be the set of all points in a plane and let O be the origin Let
R={(p,q):OP=OQ}. then ,R is
View Solution
