Let ABC be a triangle such that AB=BC. Let F be midpoint of AB and X be a poin on BC such that FX is perpendicular to AB. If BX =3XC then the ratio BC/AC equals

A

$\sqrt{3}$

B

$\sqrt{2}$

C

$\sqrt{\frac{3}{2}}$

D

1

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

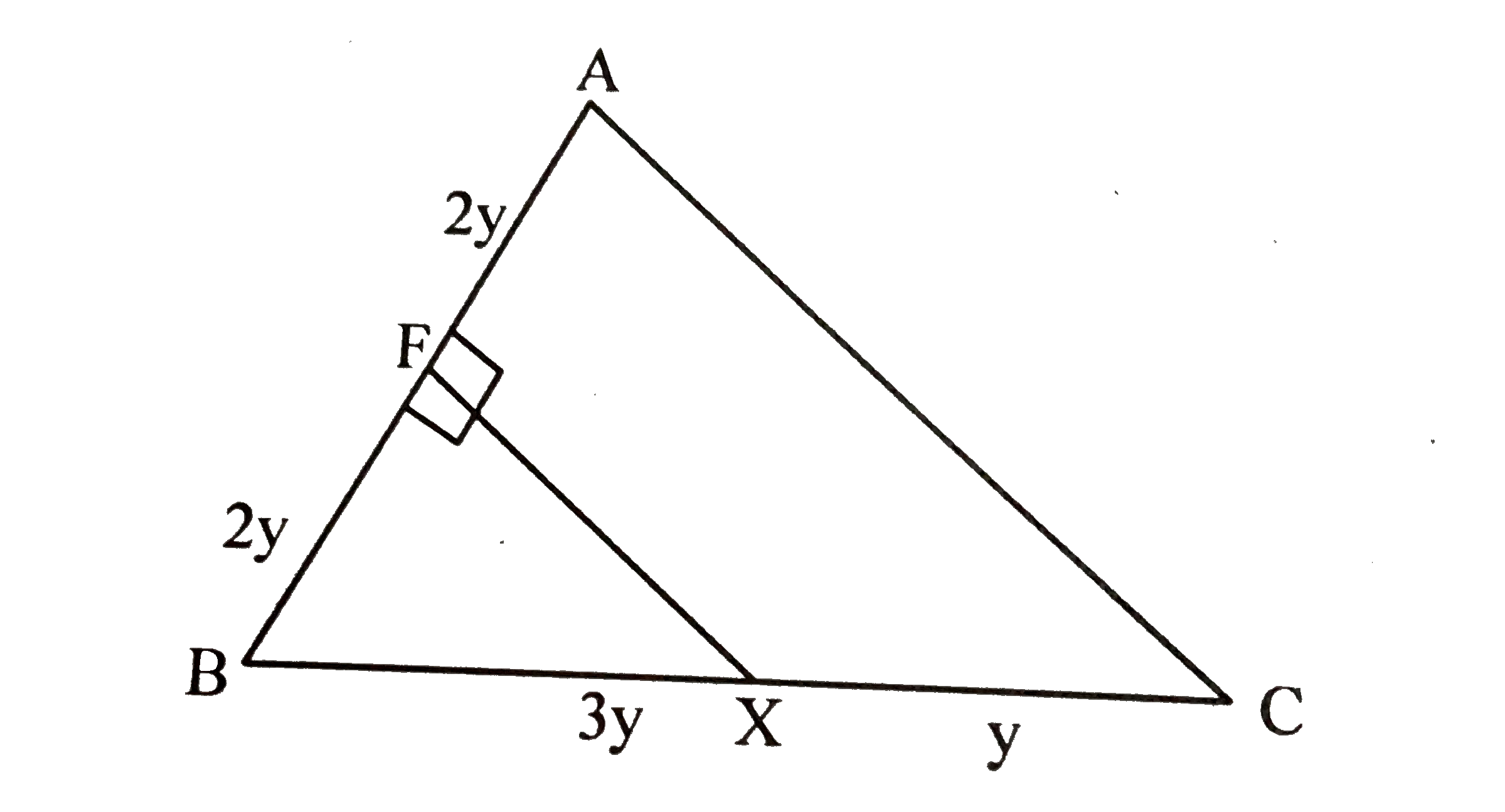
$∴ Cos B = \frac{2}{3}$
Also $cos B = \frac{16 y^{2} + 16 y^{2} - A C^{2}}{2.4 y .4 y}$
$\frac{2}{3} = \frac{32 y^{2} - A C^{2}}{32 y^{2}}$
$64 y^{2} = 96 y^{2} - 3 A c^{2}$
$3 A C^{2} = 32 y^{2}$
$A C = \frac{4 \sqrt{2}}{\sqrt{3}} y$
$∴ \frac{B C}{A C} = \frac{4 y}{(\frac{4 \sqrt{2} y}{\sqrt{3}})} = \frac{\sqrt{3}}{\sqrt{2}}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In triangle ABC, AD is prependicular to BC and DE is perpendicular to AB

A $\begin{matrix} a & b & c & d p & r & q & q \end{matrix}$
B $\begin{matrix} a & b & c & d q & r & p & s \end{matrix}$
C $\begin{matrix} a & b & c & d s & p & q & r \end{matrix}$
D $\begin{matrix} a & b & c & d r & p & s & q \end{matrix}$
Question 2 - Select One
Let ABC be an acute-angled triangle and let D be the midpoint of BC. If AB = AD, then tan(B)/tan(C) equals
A $\sqrt{2}$
B $\sqrt{3}$
C $2$
D3
Question 3 - Select One
In $Δ A B C, A B = A C, O$ is a point on BC such that BO = CO and OD is perpendicular to AB and OE is perpendicular to AC. If $∠ B O D = 30^{\circ}$ then measure of $∠ A O E$ is
A $45^{\circ}$
B $60^{\circ}$
C $75^{\circ}$
D $30^{\circ}$

KVPY PREVIOUS YEAR-KVPY-PART -I MATHEMATICS

Home
Ask Doubt
Profile