Two persons A and B throw a (fair) die (six faced cube faces numbered from 1 to 6 ) alternately, starting with. A the first person to get an outcome different from the pervious one by the opponent wins. The probability than B wins is
56
67
78
89
The correct Answer is:B
P=66⋅56+66⋅16⋅16⋅56+66⋅16⋅16⋅16⋅16⋅56+....∞
=56+563+565+....
=5/61−136=3035=67
Topper's Solved these Questions
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:PART-II MATHEMATICS
Explore 10 Videos
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:Part A - Mathematics
Explore 20 Videos
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:PART-2(MATHEMATICS)
Explore 10 Videos
- KVPY 2021Book:KVPY PREVIOUS YEARChapter:KVPY 2021Exercise:PART II MATHEMATICS
Explore 4 Videos
Similar Questions
Two person AandB take turns in throwing a pair of dice. The first person to through 9 from both dice will win the game. If A throwns fisrt then the probability that B wins the game is.
View SolutionAandB alternately throw with a pair of dice. Who gets a sum of 7 points 1st will win the game. If A starts the game, the probability of his winning is
View Solution
Knowledge Check
A die with faces numbered from 1 to 6 is thrown twice. The probability, that the numbers shown up differ by 2. is
A19B29C39D49Two different positions of the same dice are shown, the six faces of which are numbered from 1 to 6. Select the number that will be on the face opposite to the one having ‘5’
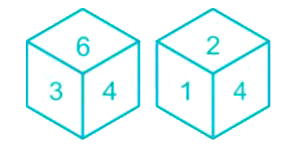 A2B3C4D6
A2B3C4D6Two different positions of the same dice are shown ,the six faces which are numbered from 1 to 6 . Select the number that will be on the face opposite to the face showing 3.
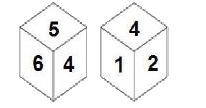 A(A). 2B(B). 5C(C). 1D(D). 4
A(A). 2B(B). 5C(C). 1D(D). 4
A fair coin is tossed. If head appears, a fair dice is tossed once and the number on the upper face noted. If tail appears, the fair dice is tossed twice independently and the sum on the upper faces is noted. Then the probability that the noted number is 3, is
(A)1/18 (B)1/4 (C)1/6 (D)1/9
View SolutionTwo persons A and B throw a coin alternatively till one of them gets head and wins the game. Find their respective probabilities of winning.
View SolutionTwo persons A and B throw a die alternately till one of them gets a three and wins the game. Find their respectively probabilities of winning, if a begins.
View SolutionHow many liters of pure acid are there in 8 liters of a 20% solution?
View SolutionTwo persons A and B throw a die alternatively till one of them gets a three and wins the game. Find their respective probabilites of winning.
View Solution
