ABC is an isosceles right anlged triangle with AB = BC = 1 . If P is any point on AC, then min (max {(area APQ) , (area PQBR) , area PRC )}} is
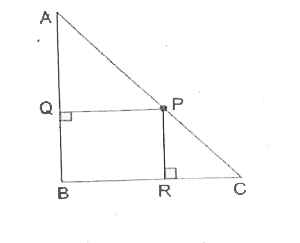
A
29
B
19
C
13
D
none of these
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - Exercise 1
3 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - Exercise 2
4 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
12 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Comprehension Type
6 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
328 Videos
Similar Questions
Knowledge Check
ABC is a right isosceles triangle with ∠B=90∘. If length of median from B to AC is 6 cm then area of triangle is
A9cm2B72cm2C36cm2D18cm2
ABC is an isosceles triangle with AC = BC. If AB2−2AC2=0, prove that ABC is right triangle.
View SolutionΔABC is an isosceles, with AB=AC. If P be any point on the side BC. Prove that AP<AB.
View SolutionABC is an isosceles triangle with AC=BC . If AB2=2 AC2 , prove that ABC is right triangle.
View SolutionABC is an isosceles triangle with AC = BC. If AB2=2AC2, prove that ABC is a right triangle.
View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View SolutionABC is a right-angled triangle at A. Semicircles drawn on AB, AC and BC as diameters. Find area of the shaded region.

View Solution

