An ellipstical cavity is made within a perfect conductor. A positive charge q is placed at the centre of the cavity. The points A and B are on the cavity surface as shown in the adjacent figure. Then,

electric field near A in the cavity = electric field near B in the cavity
charge density at A = charge density at B
potential at A = potential at B
total electric field flux through the surface of the cavity is q/ε0
All the points which lie on the conductor are at the same potential
Again, according the Gauss' law, net flux through the surface of cavity = qε0
Topper's Solved these Questions
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - EXERCISE
10 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL - I
14 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
10 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
21 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
Similar Questions
An ellipsoidal cavity is carved within a perfect conductor. A positive charge q is placed at the centre of the cavity. The points A and B are on the cavity surface as shown in the figure. Then
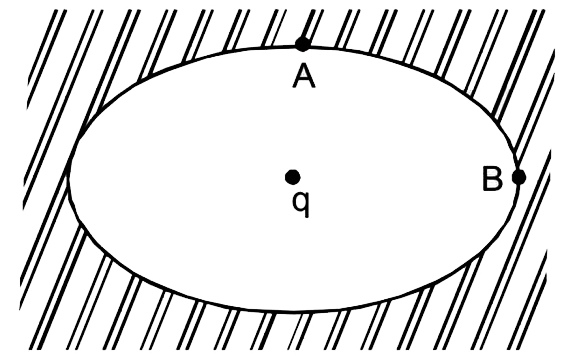
View SolutionAn ellipsoidal cavity is carved with in a perfect conductor. A positive charge q is placed at the centre of the cavity. The points A and B are on the cavity surface as shown in the figure then
(a) Electric field near A in the cavity = Electric field near B in the cavity
(b) Charge density at A= Charge density at B
(c ) Potential at A= Potential at B
(d) Total electric flux through the surface of the cavity is q/ε0.
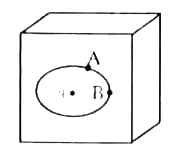
View Solution
Knowledge Check
An ellipsoidal cavity is carved within a perfect conductor. A positive charge q is placed at the centre of the cavity. The points A and B are on the cavity surface as shown in the figure. Then
 Aelectric field near A in the cavity = electric field near B in the cavityBcharge density at A= charge density at BCpotential at A=potential at BDtotal electric field flux through the surface of the cavity is q/ε0
Aelectric field near A in the cavity = electric field near B in the cavityBcharge density at A= charge density at BCpotential at A=potential at BDtotal electric field flux through the surface of the cavity is q/ε0There is a cubical cavity inside a conducting sphere of radius R. A positive point charge Q is placed at the centre of the cube and another positive charge q is placed at a distance 1(>R) from the centre of the sphere. The sphere is earthed
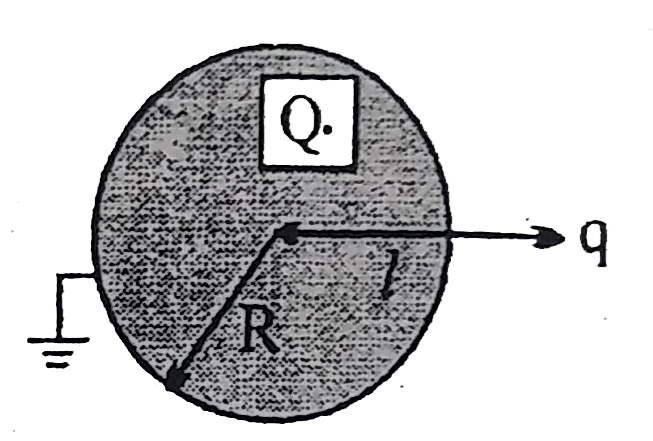
Net charge on the outer surface of conducting sphere isA+QBQ−qR/1C−qR/IDnoneA charge Q0 is placed at the center of spherical cavity of a conductor and another charge Q is placed outside the conductor as shown in the figure. The correct statement is :
 AForce on Q0 and Q are equal and oppositeBForce on Q0 is zero and force on Q is nonzeroCForce on Q and Q0 is zeroDForce on Q0 is nonzero and force on Q is zero
AForce on Q0 and Q are equal and oppositeBForce on Q0 is zero and force on Q is nonzeroCForce on Q and Q0 is zeroDForce on Q0 is nonzero and force on Q is zero
A solid spherical conductor of radius R has a spherical cavity inside it (see figure). A point charge q is placed at the centre of the cavity. (a) What is the potential of the conductor? (b) If the charge q is shifted inside the cavity by a distance Δx, how does the potential of the conductor change? (c) How does your answer to the question (a) and (b) change if the cavity is not spherical and the charge q is placed at any point inside it (see figure) (d) Draw electric field lines in entire space in each case. In which case all field lines are straight lines
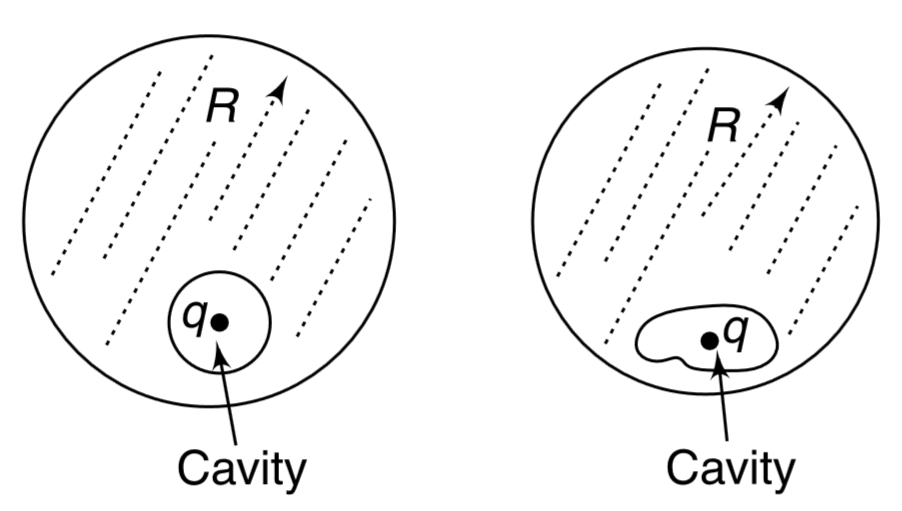
View SolutionA spherical metallic conductor has a spherical cavity. A positive charge is placed inside the cavity at its centre. Another positive charge is placed
View SolutionA spherical cavity of radius r is made in a conducting sphere of radius 2 r.A charge q is kept at the centre of cavity as shown in the figure.Find the magnitude of the total electric field at (4r 0) .
View SolutionThere is a conductor with cavity of radius R as shown in figure. A point charge Q is placed at R/2 distance from centre of cavity.
A point P is at r distance from centre of conductor. Then,

View SolutionAsseration: A point charge q is placed at centre of spherical cavity inside a spherical conductor as shown. Another point charge Q is placed outside the conductor as shown. Now as the point charge Q is pushed away from conductor, the potential difference (VA−VB) between two points A and B within the cavity of sphere remains constant.

Reason: The electric field due to charges on outer surface of conductor and outside the conductor is zero at all points inside teh conductor.
View Solution
