Question

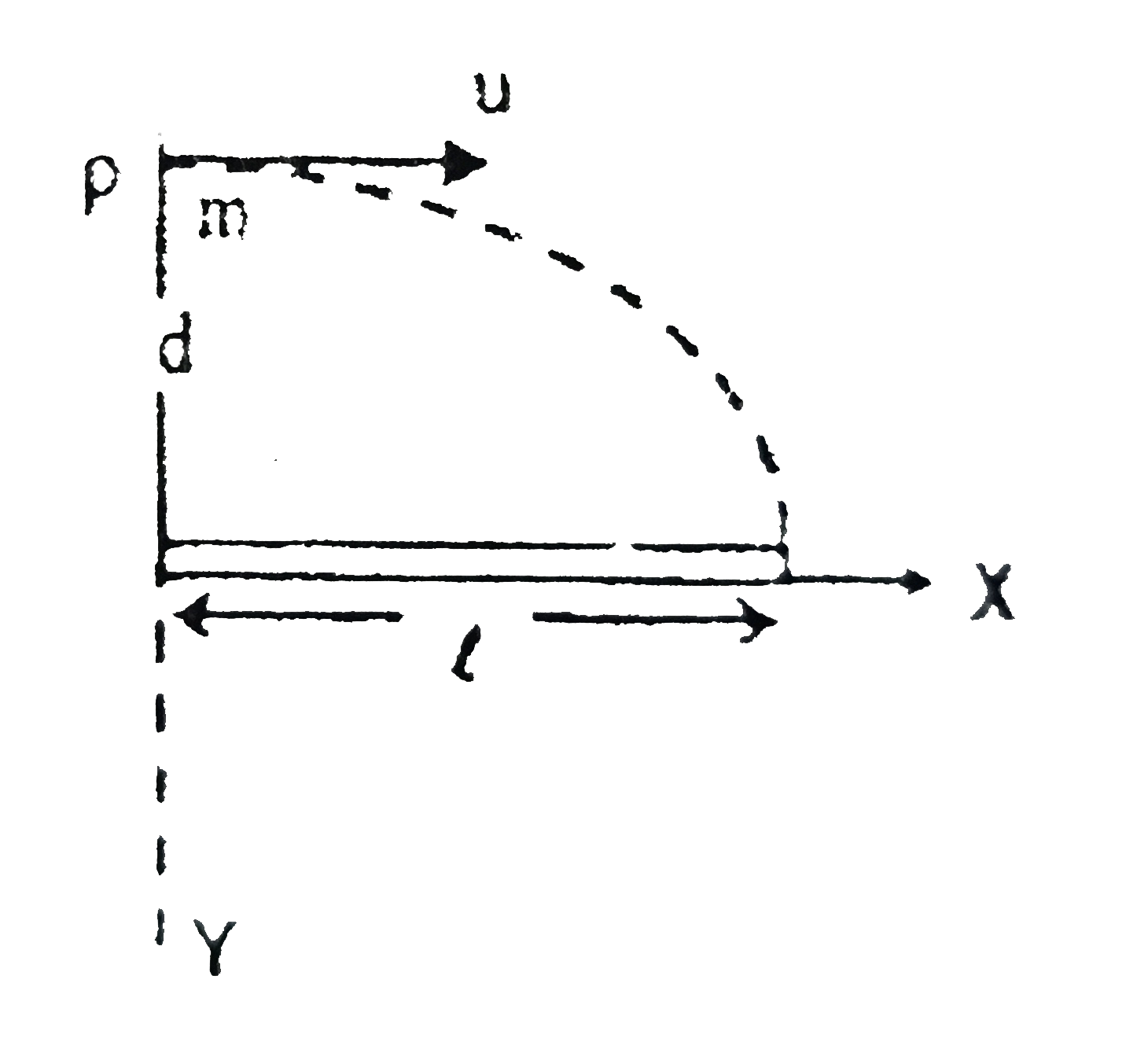
An electron is projected from a distance d and with initial velocity u parallel to a uniformly charged flat conducting plate as shown. It strikes the plate after travelling a distance l long the direction of projection. The surface charge density of the conducting plate is equal to

Options

A. `(2depsilon_(0)m u^(2))/(el^(2))`
B. `(2depsilon_(0)m u)/(el)`
C. `(depsilon_(0)m u^(2))/(el)`
D. `(depsilon_(0)m u)/(el)`

Explanation

For the motion of the electon along Y axis
`d=(1)/(2)(eE)/(m)t^(2)" "...(1)`
Where E is the electric field due to the charged plate given by
`E=(sigma)/(epsilon_(0))" "...(2)`
`sigma` is the surface density of charge of the plate.
The time taken by the electron is
`t=(l)/(u)" "...(3)`
From (1), (2) and (3) we obtain,
`d=(1)/(2)(esigma)/(epsilon_(0)m)((l)/(u))^(2)impliessigma=(2depsilon_(0)m u^(2))/(el^(2))`