A metallic sphere of radius is covered with a dielectric substance of varying dielectric the dielectric constant as a function of the radial distance from the centre of the sphere $k = k_{0} {(1 + \frac{r}{a})}^{- 1} (a \leq r \leq 2 a)$ .
Find the capacitance of the metallic sphere. The dielectric extends upto a radial distance r = 2a.

Text Solution

Verified by Experts

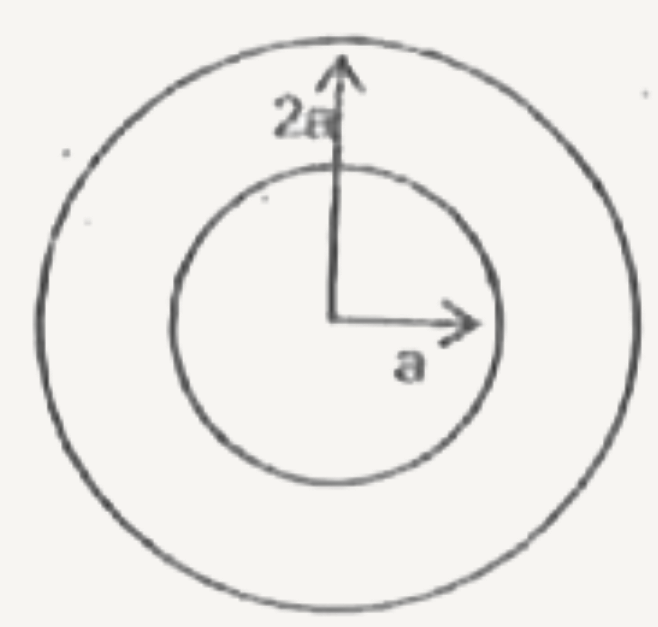
$4 π ε_{0} a k_{0} {[1 + ln 2]}^{- 1}$

Updated on:21/07/2023

The capacitance of a capacitor, filled with two dielectrics of same dimensions but of dielectric constants $K_{1} and K_{2}$ respectively as shown will be -
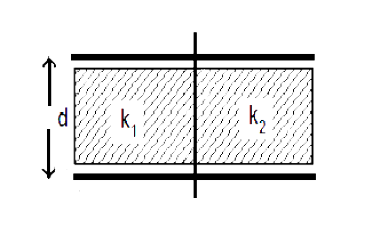A $\frac{\in_{0} A}{2 d} (K_{1} + K_{2})$
B $\frac{\in_{0} A}{d} (K_{1} + K_{2})$
C $\frac{\in_{0} A}{2 d} (\frac{K_{1} + K_{2}}{K_{1} + K_{2}})$
D $\frac{\in_{0} A}{d} (\frac{K_{1} K_{2}}{K_{1} + K_{2}})$
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
Adecreases as r increases for $r < R$ and $r > R$
Bincreases as r increases for $r < R$ and $r > R$
Czero as r increases for $r < R$ , decreases as r increases for $r > R$
Dzero as r increases for $r < R$ , increases for $r > R$
A capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant $K_{1} = 6 and K_{2} = 4$ . New capacitance will be

A $4 \frac{A ε_{0}}{d}$
B $4.8 \frac{A ε_{0}}{d}$
C $5 \frac{A ε_{0}}{d}$
D $2.4 \frac{A ε_{0}}{d}$