For a uniformly charged sphere electric field $\vec{E}$ inside the sphere is given as $\vec{E} = \frac{ρ}{3 ε_{0}} (\vec{r})$ , where $ρ$ is volume charge density and $\vec{r}$ is the position vector of the point with respective to centre For a given charge distribtution if the electric field at a point (P) is ${\vec{E}}_{1}$ , and now some part of charge distribution is removed to form a cavity, electric field at same point (P) only due to removed part is ${\vec{E}}_{2}$ . Then finally electric field at point P is ${\vec{E}}_{3} = {\vec{E}}_{1} - {\vec{E}}_{2}$ .
There is a uniformly charged sphere of volume charge density $ρ$ and radius R with a cavity of radius $(R / 2)$ as shown in the diagram.

ocr_image

Text Solution

Verified by Experts

See it carefully that electric field is same throughout the volume of cavity and equal to that at centre

The electric field due to a uniformly charged sphere is maximum at :
Acentre of sphere
Binside the surface
Cat the surface
Dat infinite distance from the centre
A hollow sphere of copper is positively charged. Then the electric field inside the sphere is
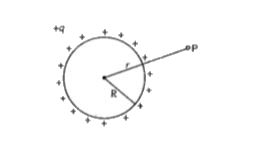
Athe same as the field at the surface
Bgreater than the field at the surface
Cess than the field at the surface but not zero
Dzero
Electric field intensity at point P due to charge distributed over a sphere is:

A $E = \frac{1}{4 π ε_{0}} \frac{q}{r}$
B $E = \frac{σ R^{2}}{ε_{0} r^{2}}$
C $E = \frac{1}{4 π ε_{0}} \frac{q}{r}$
D $E = 0$