Find the electric field at an arbitrary point of a sphere carrying a charge uniformly distributed over its volume.

वीडियो समाधान

लिखित उत्तर

Verified by Experts

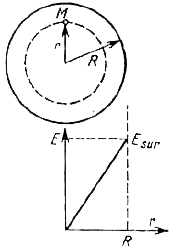
Let the volume density of the charge $ρ = \frac{Q}{V} = \frac{3 Q}{4 π R^{3}}$ , where R is the radius of the sphere. Choose a point M Inside the spliere al a distance $r < R$ from its centre and consider a concentric sphere through it. From the results obtained in Problem 24.13 it is evident that the spherical layer lying outside point M does not create a field at this point. The field is created solely by the charge $q = \frac{4}{3} π r^{3} ρ$ contained inside the smaller sphere. By the result of the previous problem, the field at the surlace of this sphere, 1.e. at point M, will be
$E = \frac{q}{4 π ε_{0} r^{2}} = \frac{4 π r^{3} ρ}{3 \times 4 π ε_{0} r^{2}} = \frac{ρ r}{3 ε_{0}}$
We see that the field inside the sphere increases in proportion to the radius, at the centre its i tensity is zero, and on the surface it is
$E_{sur} = \frac{ρ R}{3 ε_{0}} = \frac{Q}{4 π ε_{0} R^{2}}$
This dependence is plotted in Fig. 24.15. 24.16. The feld potentials on the surfaces of both spheres are $φ = q / (4 π ε_{0} R), φ_{0} = q / (4 π ε_{0}, R_{1})$ respectively. The potential difference is
$φ - φ_{1} = \frac{q}{4 π ε_{0}} (\frac{1}{R} - \frac{1}{R_{1}}) = \frac{q R (_(1) - R)}{4 π ε_{0} R R_{1}}$
The Capacitance is $C = \frac{q}{φ - φ_{1}} = \frac{4 π ε_{0} R R_{1}}{R_{1} - R_{2}}$
If $d = R_{1} - R l r < R$ , we obtaine the approximation $C = \frac{4 π ε_{0} R^{2}}{d} = \frac{ε_{0} S}{d}$
which is the expression for the capacitance of a plane capacitor. The error is
$δ = \frac{C_{s p} - C_{p l}}{C_{a p}} = \frac{R_{1} - R}{R} = \frac{d}{R}$

Updated on:21/07/2023

|

Class 12 PHYSICS A FIELD OF FIXED CHARGES IN A VACUUM

समान प्रश्न

Recommended Questions

Home
Ask Doubt
Profile