Taken on side ¯¯¯¯¯¯AC of a ΔABC, a point M such that ¯¯¯¯¯¯¯AM=13¯¯¯¯¯¯AC. A point N is taken c the side BC such that ¯¯¯¯¯¯BN=¯¯¯¯¯¯CB, then for the point of intersection X of ¯¯¯¯¯¯AB and ¯¯¯¯¯¯¯¯MN, which of the following is true
A
¯¯¯¯¯¯XB=13¯¯¯¯¯¯AB
B
¯¯¯¯¯¯AX=13¯¯¯¯¯¯AB
C
¯¯¯¯¯¯¯XN=34¯¯¯¯¯¯¯¯MN
D
¯¯¯¯¯¯¯XM=3¯¯¯¯¯¯¯XN
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- MATHEMATICS TIPSBOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - ASSERTION - REASONING
8 Videos
- MATHEMATICS TIPSBOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - MCQ (MULTIPLE CORRECT)
30 Videos
- MATHEMATICS TIPSBOOK - FIITJEECHAPTER - MATHEMATICS TIPSEXERCISE - ASSIGNMENT (SECTION (I) : MCQ (SINGLE CORRECT)
120 Videos
- MATHEMATICS BOOK - FIITJEECHAPTER - MATHEMATICS EXERCISE - NUMERICAL DECIMAL BASED QUESTIONS
15 Videos
- MATRICES BOOK - FIITJEECHAPTER - MATRICES EXERCISE - NUMERICAL BASED
3 Videos
Similar Questions
Knowledge Check
In △ABC,∠B=90∘, P,Q and R are the mid-points of ¯¯¯¯¯¯AB,¯¯¯¯¯¯BC and ¯¯¯¯¯¯AC respectively. Then which of the following is true?
AA,P,Q and R are concylic points.BB,P,R and Q are concylic points.CC,Q,P and R are concyclic points.DAll of thesePoint A, B, and C all lie on a line. Point D is midpoint of ¯¯¯¯¯¯AB and E is the midpoint of BC,¯¯¯¯¯¯AB=4and¯¯¯¯¯¯BC=10. Which of the following could be the length of ¯¯¯¯¯¯AE?
A1B2C3D4If D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
A2(¯¯¯¯¯¯AD−¯¯¯¯¯¯BD)B2(¯¯¯¯¯¯DC−¯¯¯¯¯¯BD)C2(¯¯¯¯¯¯BD−¯¯¯¯¯¯CA)D2(¯¯¯¯¯¯BD−¯¯¯¯¯¯AC)
In the given figure ¯¯¯¯¯¯AB=¯¯¯¯¯¯BC and ¯¯¯¯¯¯AC=¯¯¯¯¯¯CD if ∠BAD=y and ∠ADB=x then ∠y=
View Solution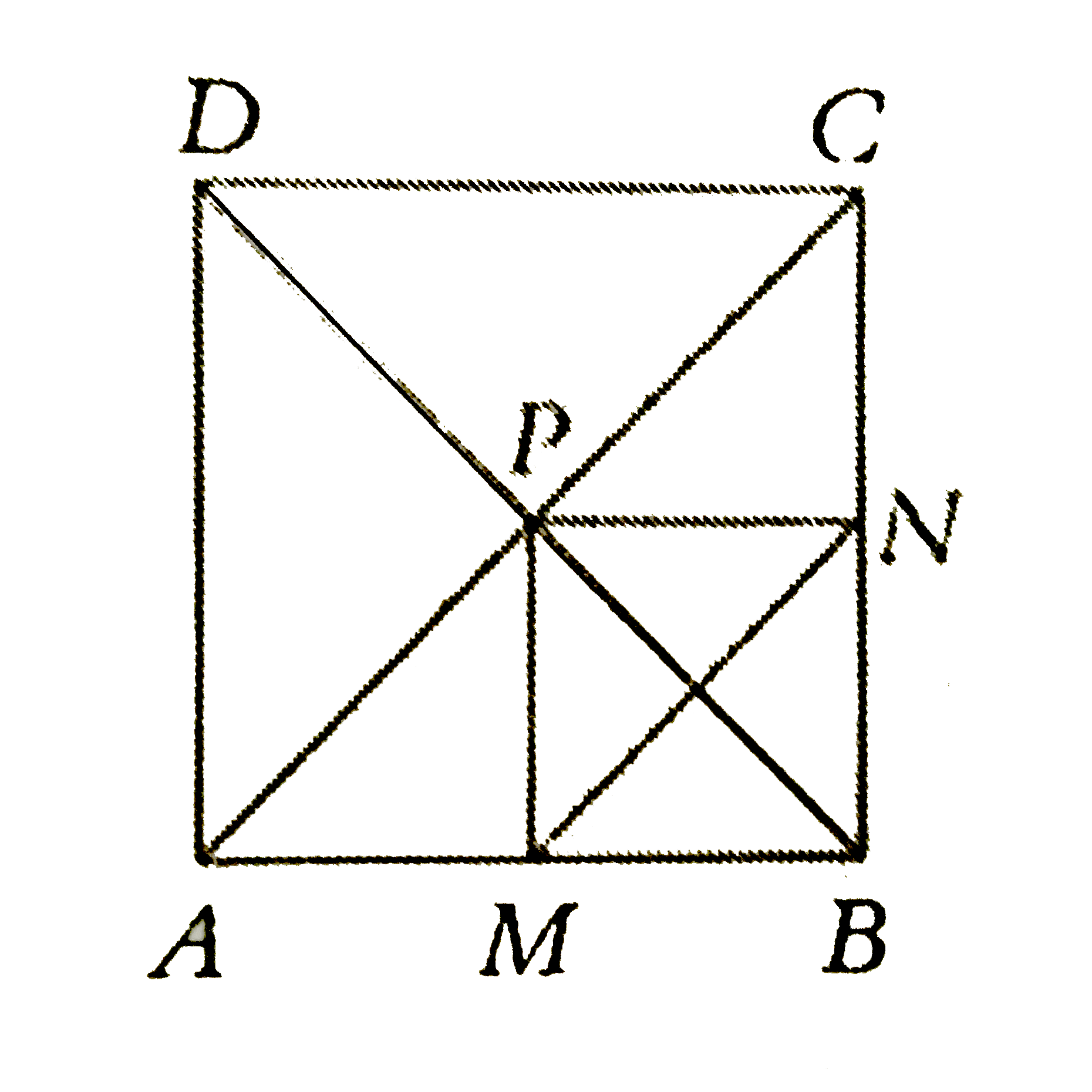
In the figure above, ABCD is a square of side 18 cm and ¯¯¯¯¯¯PN⊥¯¯¯¯¯¯BCand¯¯¯¯¯¯¯PM⊥¯¯¯¯¯¯AB. Find the length of MN.
View SolutionABCD is a parallelogram If M and N are the midpoints of BC and DC respectively,If ¯¯¯¯¯¯¯AM+¯¯¯¯¯¯AN=λ(¯¯¯¯¯¯AC) then value of λ
View SolutionIn a ΔABC,¯¯¯¯¯¯AB2+¯¯¯¯¯¯AC2=¯¯¯¯¯¯BC2 and ¯¯¯¯¯¯BC=√2¯¯¯¯¯¯AB , then ∠ABCis :
View SolutionABC is an equilateral triangle. P and Q are two points on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯AC respectively such that ¯¯¯¯¯¯PQ∣∣¯¯¯¯¯¯BC. If ¯¯¯¯¯¯PQ=5cm, then area of ΔAPQ is :
View Solution
