The relation between position (x) and time (t) are given below for a particle moving along a straight line. Which of the following equation represents uniformly accelerated motion? [where are positive constants]
The correct Answer is:D
To determine which of the given equations represents uniformly accelerated motion, we need to analyze each option by differentiating the position function x(t) to find the velocity v(t) and then differentiating the velocity to find the acceleration a(t). Uniformly accelerated motion is characterized by constant acceleration.
1. Check Option 1:
x(t)=αβt+α
- Find Velocity:
v(t)=dxdt=αβ
- Find Acceleration:
a(t)=dvdt=0
- Since the acceleration is zero (not constant), this option does not represent uniformly accelerated motion.
2. Check Option 2:
x(t)=βα+tα
- Find Velocity:
v(t)=dxdt=1α
- Find Acceleration:
a(t)=dvdt=0
- Again, the acceleration is zero (not constant), so this option also does not represent uniformly accelerated motion.
3. Check Option 3:
x(t)=αβt−1
- Find Velocity:
v(t)=dxdt=−αβt−2
- Find Acceleration:
a(t)=dvdt=2αβt−3
- The acceleration is not constant (it varies with time), so this option does not represent uniformly accelerated motion.
4. Check Option 4:
αt=√β+x
- Square Both Sides:
α2t2=β+x⟹x=α2t2−β
- Find Velocity:
v(t)=dxdt=2α2t
- Find Acceleration:
a(t)=dvdt=2α2
- The acceleration is constant (2α2), indicating that this option represents uniformly accelerated motion.
Conclusion:
The equation that represents uniformly accelerated motion is Option 4.
x(t)=αβt+α
- Find Velocity:
v(t)=dxdt=αβ
- Find Acceleration:
a(t)=dvdt=0
- Since the acceleration is zero (not constant), this option does not represent uniformly accelerated motion.
x(t)=βα+tα
- Find Velocity:
v(t)=dxdt=1α
- Find Acceleration:
a(t)=dvdt=0
- Again, the acceleration is zero (not constant), so this option also does not represent uniformly accelerated motion.
x(t)=αβt−1
- Find Velocity:
v(t)=dxdt=−αβt−2
- Find Acceleration:
a(t)=dvdt=2αβt−3
- The acceleration is not constant (it varies with time), so this option does not represent uniformly accelerated motion.
αt=√β+x
- Square Both Sides:
α2t2=β+x⟹x=α2t2−β
- Find Velocity:
v(t)=dxdt=2α2t
- Find Acceleration:
a(t)=dvdt=2α2
- The acceleration is constant (2α2), indicating that this option represents uniformly accelerated motion.
The equation that represents uniformly accelerated motion is Option 4.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)
37 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - A)
60 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
4 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
Knowledge Check
Which of the following represents the equation for position-time relation?
A2as=v2−u2Bs=ut+1/2at2Cv=u+atDV=u+atThe position of a particle moving on a straight line depends on time t as
x=(t+3)sin(2t)AIts velocity at the initial moment is 6 m/sBIts acceleration at the initial is −8m/s2CIt has velocity of 3 m/s at t=π2 secDIt has an acceleration of 2m/s2 at t=π4 secThe position (x) - time (t) graph for a particle moving along a straight line is shown in figure. The average speed of particle in time interval t = 0 to t = 8 s is
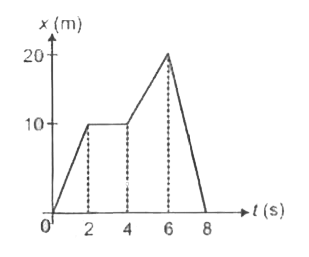 AZeroB5 m/sC7.5 m/sD9.7 m/s
AZeroB5 m/sC7.5 m/sD9.7 m/s
Acceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :

View SolutionWhich of the following relations representing displacement x (t) of particle describes motion with constant acceleration?
View SolutionPosition of a particle moving along a straight line is given by x=2t2+t . Find the velocity at t = 2 sec.
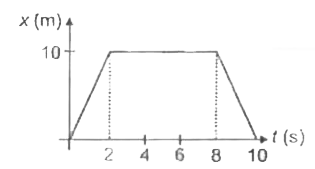
View SolutionThe position - time graph for a particle moving along a straight line is shown in figure. The total distance travelled by it in time t = 0 to t = 10 s is
View Solution