Coefficient of kinetic friction and coefficient of static friction between two blocks is μk and μs respectively. In general
μs<μk
μs>μk
μs=μk
None of these
To solve the problem regarding the relationship between the coefficients of kinetic friction (μ_k) and static friction (μ_s) between two blocks, we can follow these steps:
Step 1: Understand the Definitions
- Static Friction (μ_s): This is the frictional force that prevents two surfaces from sliding past each other when at rest. It has a maximum value known as limiting friction.
- Kinetic Friction (μ_k): This is the frictional force acting between two surfaces that are sliding past each other.
Step 2: Analyze the Graph of Applied Force vs. Friction Force
- When an external force is applied to a block at rest, the frictional force increases proportionally until it reaches a maximum value (limiting friction).
- Beyond this point, if the applied force exceeds the limiting friction, the block starts to slide, and the frictional force transitions to kinetic friction.
Step 3: Identify the Relationship
- The maximum static friction (limiting friction) can be expressed as:
Fs,max=μs⋅N
where N is the normal force.
- The kinetic friction can be expressed as:
Fk=μk⋅N
Step 4: Compare the Coefficients
- It is generally observed that:
μk<μs
- This means that the coefficient of kinetic friction is less than the coefficient of static friction.
Conclusion
Thus, in general, the coefficient of static friction (μ_s) is greater than the coefficient of kinetic friction (μ_k).
Final Answer
μs>μk
- Static Friction (μ_s): This is the frictional force that prevents two surfaces from sliding past each other when at rest. It has a maximum value known as limiting friction.
- Kinetic Friction (μ_k): This is the frictional force acting between two surfaces that are sliding past each other.
- When an external force is applied to a block at rest, the frictional force increases proportionally until it reaches a maximum value (limiting friction).
- Beyond this point, if the applied force exceeds the limiting friction, the block starts to slide, and the frictional force transitions to kinetic friction.
- The maximum static friction (limiting friction) can be expressed as:
Fs,max=μs⋅N
where N is the normal force.
- The kinetic friction can be expressed as:
Fk=μk⋅N
Step 4: Compare the Coefficients
- It is generally observed that:
μk<μs
- This means that the coefficient of kinetic friction is less than the coefficient of static friction.
Thus, in general, the coefficient of static friction (μ_s) is greater than the coefficient of kinetic friction (μ_k).
μs>μk
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Example
24 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Knowledge Check
The coefficient of static friction between two surfaces depend on
Anature of surfaceBthe shape of the surface in contactCthe area of contactDall of the aboveIf coefficient of static friction is μs and coefficient of kinetic friction is μk , which one is correct ?
Aμs=μkBμs>μkCμs<μkDμs≤μkA block of mass m2 is placed on a horizontal table and another block of mass m1 is placed on top is it. An increasing horizontal force F=αt is exerted on the upper block but the lowwer block never moves as a result. If the coefficient of friction between the blocks is μ1 coefficient of friction between the blocks is μ1 and that between the lower block and the table is μ2, then what is the maximum possible value of μ1/μ2 ?
Am2m1B1+m2m1Cm1m2D1+m1m2
When the coefficient of friction between the weight and the palte is μ.
View SolutionA block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).
View SolutionA small block of mass m is kept on the inclined surface of a wedge of mass M. The inclined surface of the wedge makes an angle θ with the horizontal. The wedge is kept on a frictionless rigid horizontal floor. You can neglect friction between the block and the wedge also. An external agent applies a horizontal force F on the wedge.
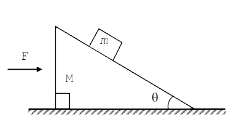
The value of the force F so that the wedge remains at rest is F1. Which of the options is incorrect?
View SolutionIn Fig the block are at rest a force of 10N act on the block of 4kg mass .The coefficient of staic friction and the coefficient of kinetic friction are μs=0.2andμs=0.15 for both the surface in contact The magnitudeof frcition force acting between the surface of contact between the 2kg and 4kg block in this situation is

View Solution
A force F=2t is spplied at t=0 sec to the block of mass m placed on a rough horizontal surface. The coefficient of static and kinetic friction between the block and surface are μS and μk rspectively. Which of the following graphs best represents the acceleration vs time of the block(μS>μk)?
View Solution