If μk is the coefficient of kinetic friction and μs the coefficient of static friction then generally
The correct Answer is:A
Conceptual
Topper's Solved these Questions
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - III
20 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
Similar Questions
Knowledge Check
If μk is the coefficient of kinetic friction, μl is the coefficient of rolling friction and us is the coefficient of static friction, then
Aμs>μk>μrBμs<μk<μrCμs<μr<μkDμsμr>μkA block A kept on a rough plate (OOI) with coefficient of static friction μs=0.75 & coefficient of kinetic friction μˆk=0.5. The plate is leaning with horizontal at an angle θ=tan−1(μ's). If the plate is further tilted slightly then the acceleration of block will be :
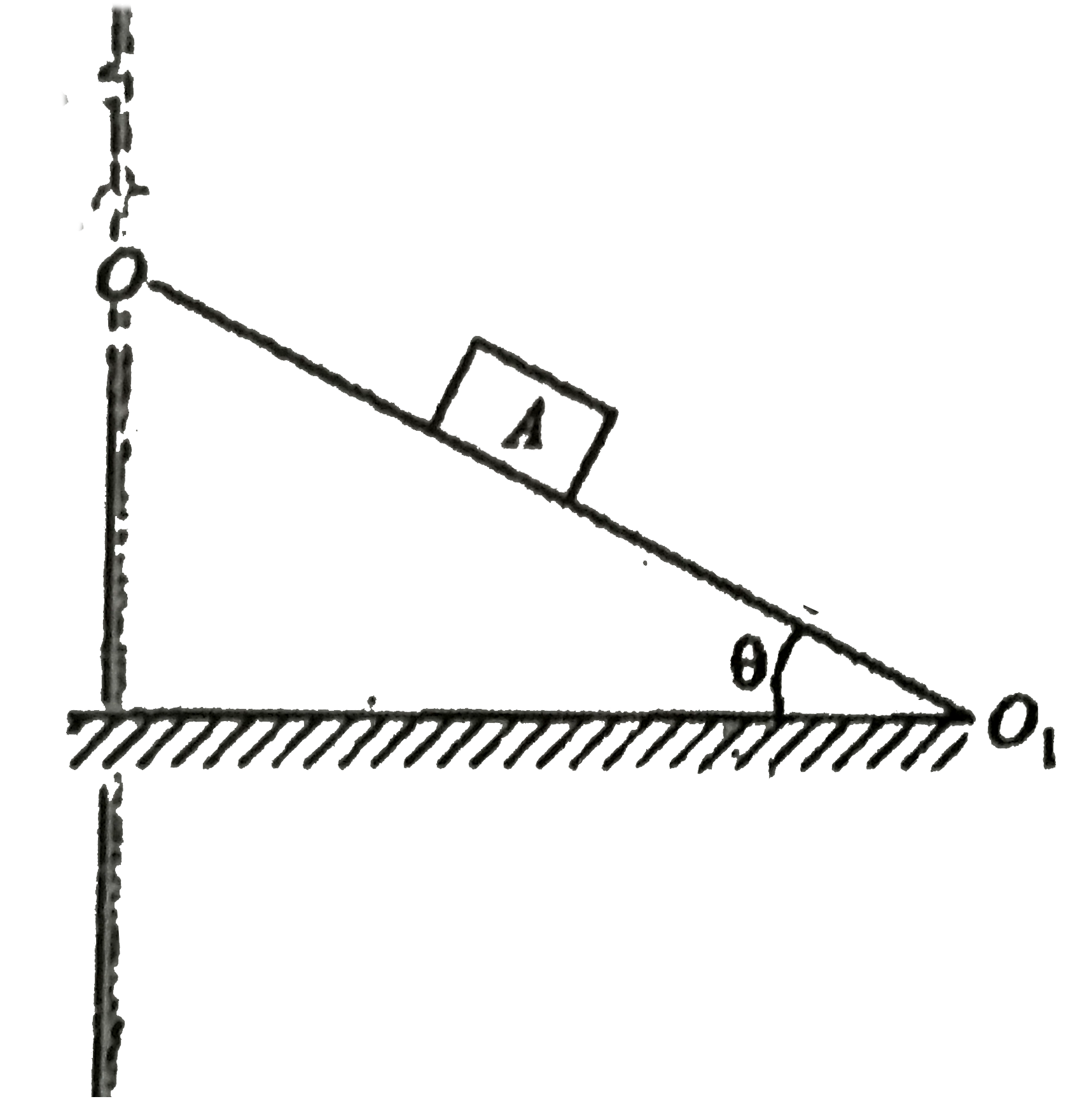 A1.5m/s2B2m/s2C2.5m/s2DNone of these
A1.5m/s2B2m/s2C2.5m/s2DNone of theseIf coefficient of static friction is μs and coefficient of kinetic friction is μk , which one is correct ?
Aμs=μkBμs>μkCμs<μkDμs≤μk
A block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).
View SolutionA block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).
View SolutionDefine the coefficient of static friction and kinetic friction.
View SolutionA small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of hte resultant force on the coin exerted by the disc just before it starts slipping on the disc is :
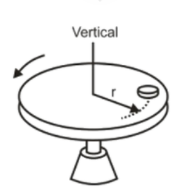
View SolutionThe ratio of μk (kinetic friction) and μs (state friction) is
View Solution
