From the data given below, find the number of items (N), r=0.5,∑xy=120, Standard Deviation of Y(σy)=8,∑x2=90 where , x and y are deviations from arithmetic mean.
Given :r=0.5,∑xy=120,∑x2=90,σy=8
Now, σy=√∑y2N
when y=Y−¯¯¯Y [formula of Standard Deviation ]
8=√∑y2N
Squaring both sides, we get
64=∑y2N⇒∑y2=64N
Now, r=∑xy√∑x2×∑y2
⇒0.5=120√90×64N
Squaring both sides
0.25=(120)290×64N
⇒0.25=14,4005,760N
⇒(0.25)(5,760)N=14,400
⇒(1,440)N=14,400
∴N=14,4001,440=10
Number of Items=10
Topper's Solved these Questions
- BOOK - TARUN JAIN & VK OHRICHAPTER - CORRELATIONEXERCISE - Learning by doing5videos
CORRELATION
- BOOK - TARUN JAIN & VK OHRICHAPTER - CORRELATIONEXERCISE - Objective type questions9videos
CORRELATION
- BOOK - TARUN JAIN & VK OHRICHAPTER - CONCEPT OF ECONOMICS AND SIGNIFICANCE OF STATISTICS IN ECONOMICSEXERCISE - NCERT Questions6videos
CONCEPT OF ECONOMICS AND SIGNIFICANCE OF STATISTICS IN ECONOMICS
- BOOK - TARUN JAIN & VK OHRICHAPTER - DIAGRAMMATIC PRESENTATION OF DATA BAR DIAGRAMS AND PIE DIAGRAMSEXERCISE - NCERT Question (With Hints to Answers)3videos
DIAGRAMMATIC PRESENTATION OF DATA BAR DIAGRAMS AND PIE DIAGRAMS
Similar Questions
If r=0.25,∑xy=45,σy=3,∑x2=50, where x and y denote deviation from their respective means, find the number of items.
View SolutionGiven r=0.8,Σxy=60,σy=2.5andΣx2=90. Find the number of items (x and y are deviations from arithmetic average)
View Solution
(ii)Find the mean deviation of numbers 3,4,5,6,7 from mean.View SolutionFind out mean deviation and coefficient of mean deviation, using arithmetic mean from the following data:
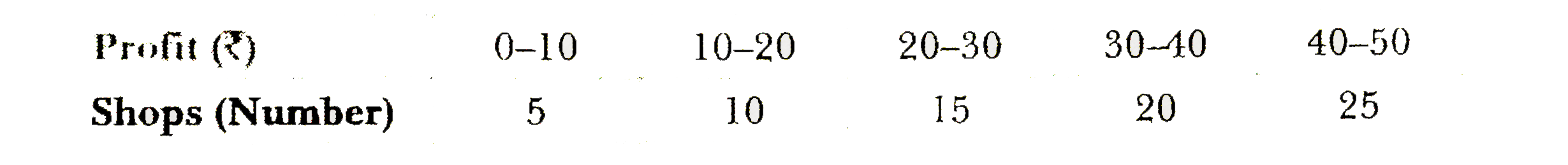 View Solution
View SolutionFind the standard deviation from the following datas, using assumed mean:
 View Solution
View SolutionFind the standard deviation from the following datas, using assumed mean:
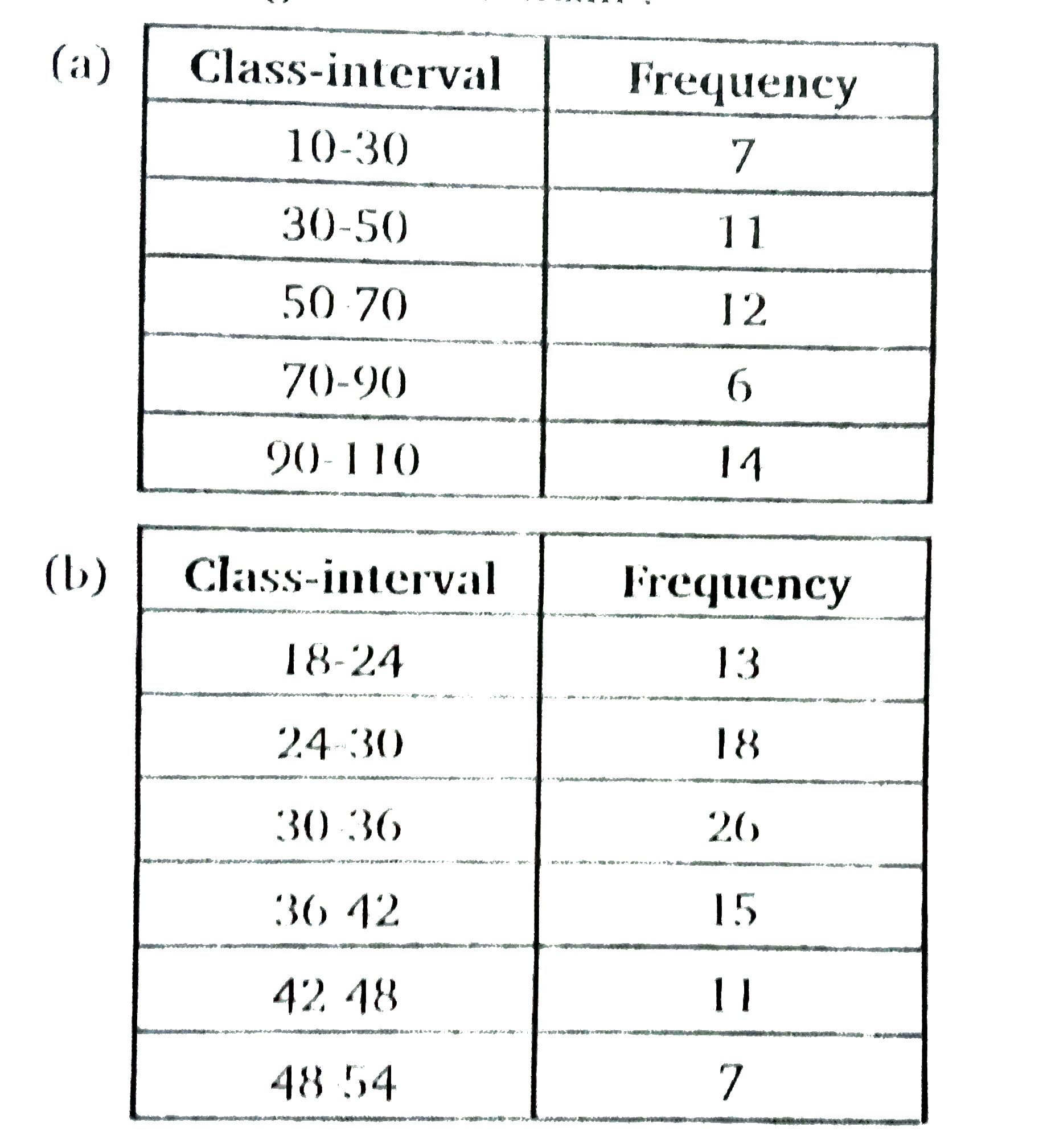 View Solution
View SolutionStatement-1 : The mean deviation of the numbers 3,4,5,6,7 is 1.2
Statement-2 :mean deviation =Σni=1|xi−¯x|n.View SolutionUsing Short-cut Method,calculate the standard deviation from the data given below:
 View Solution
View SolutionFor a group containing 100 observations, the arithmetic mean and standard deviation are 8 and √10.5. For 50 observations selected from the 100 observations, the arithmetic mean and standard deviations are 10 and 2 respectively. Find the arithmetic mean and the standard deviation of the other half.
View SolutionFrom the following data, compute the coefficient of correlation between X and Y series.
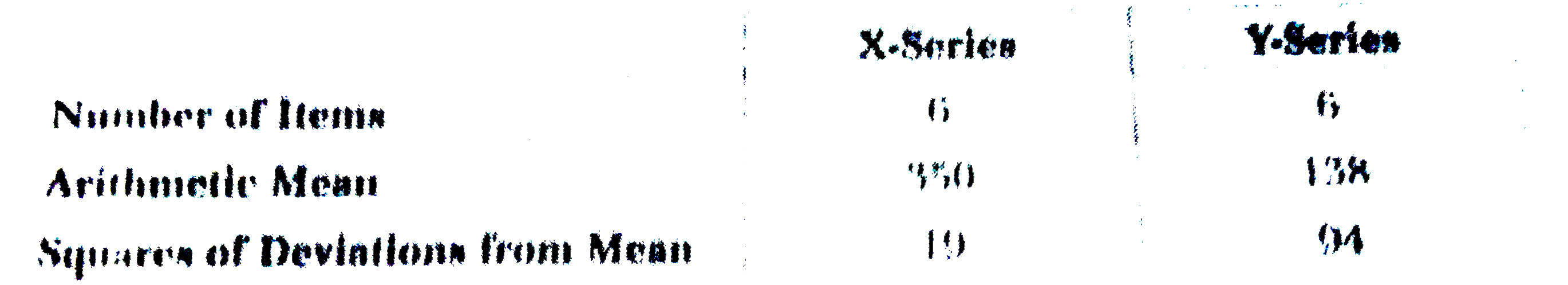
Summation of product of deviations of X and Y series from their respective arithmetic mean =41View Solution

