The coefficient of static friction between the box and the train's floor is 0.2. The maximum acceleration of the train in which a box lying on its floor will remain stationary is (Take g=10ms−2)
2ms−2
4ms−2
6ms−2
8ms−2
The correct Answer is:A
To solve the problem, we need to find the maximum acceleration of the train such that the box remains stationary relative to the train. We will use the concept of static friction.
1. Identify the Given Values:
- Coefficient of static friction (μ_s) = 0.2
- Acceleration due to gravity (g) = 10 m/s²
2. Understand the Forces Acting on the Box:
- The weight of the box (W) acts downward and is given by:
W=mg
- The normal force (N) acting on the box is equal to its weight when the box is resting on the train's floor:
N=mg
3. Determine the Maximum Static Friction Force:
- The maximum static friction force (F_friction) that can act on the box is given by:
Ffriction=μs⋅N=μs⋅mg
- Substituting the value of N:
Ffriction=μs⋅mg=0.2⋅mg
4. Relate the Forces to the Acceleration of the Train:
- For the box to remain stationary relative to the train, the maximum static friction force must be equal to the force required to accelerate the box. This force is given by:
F=ma
- Setting the two forces equal gives:
ma≤μs⋅mg
5. Simplify the Equation:
- We can cancel the mass (m) from both sides (assuming m ≠ 0):
a≤μs⋅g
6. Substitute the Values:
- Now substituting the values of μ_s and g:
a≤0.2⋅10
- This simplifies to:
a≤2m/s2
7. Conclusion:
- The maximum acceleration of the train in which the box will remain stationary is:
a=2m/s2
Final Answer:
The maximum acceleration of the train is 2 m/s².
- Coefficient of static friction (μ_s) = 0.2
- Acceleration due to gravity (g) = 10 m/s²
- The weight of the box (W) acts downward and is given by:
W=mg
- The normal force (N) acting on the box is equal to its weight when the box is resting on the train's floor:
N=mg
- The maximum static friction force (F_friction) that can act on the box is given by:
Ffriction=μs⋅N=μs⋅mg
- Substituting the value of N:
Ffriction=μs⋅mg=0.2⋅mg
- For the box to remain stationary relative to the train, the maximum static friction force must be equal to the force required to accelerate the box. This force is given by:
F=ma
- Setting the two forces equal gives:
ma≤μs⋅mg
- We can cancel the mass (m) from both sides (assuming m ≠ 0):
a≤μs⋅g
- Now substituting the values of μ_s and g:
a≤0.2⋅10
- This simplifies to:
a≤2m/s2
- The maximum acceleration of the train in which the box will remain stationary is:
a=2m/s2
The maximum acceleration of the train is 2 m/s².
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Circular Motion14videos
LAWS OF MOTION
- BOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Solving Problem In Mechanics16videos
LAWS OF MOTION
- BOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Equilibrium Of A Particle6videos
LAWS OF MOTION
- BOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
The coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)
 View Solution
View SolutionA box, heavier than you is placed on a rough floor. The coefficient of static friction between the box and the floor is the same as that between your shoes and the floor. Can you displace the box across.the floor.
View Solution
Knowledge Check
- Question 1 - Select One
Maximum acceleration of the train in which a box lying on its floor will ramain stationary, is
[μs=0.15,g=10m/s2]A70m/s2B10.5m/s2C7.1m/s2D1.5m/s2 - Question 2 - Select One
A box of mass 2 kg is placed on the roof of a car. The box would remain stationary until the car attains a maximum acceleration. Coefficient of static friction between the box and the roof of the car is 0.2 and 1g=10 ms−2.
The maximum acceleration of the car, for the box to remain stationary, isA8 ms−2B6 ms−2C4 ms−2D2 ms−2 - Question 3 - Select One
A box of mass 2 kg is placed on the roof of a car. The box would remain stationary untill the car attains a maximum acceleration. Coefficient of static friction between the box and the roof of the car is 0.2 and g = 10ms−2. This maximum acceleration of the car, for the box to remain stationary, is
A8ms−2B6ms−2C4ms−2D2ms−2
A block of mass 5 kg is (i) pushed in case (A) and (ii) pulled in case (B), by a force F = 20 N, making an angle of 30∘ with the horizontal, as shown in the figures. The coefficient of friction between the block and floor is μ=0.2 . The difference between the accelerations of the block, in case (B) and case (A) will be: (g=10ms−2)
 View Solution
View SolutionBlock B lying on a table weighs w. The coefficient of static friction between the block and the table is mu. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
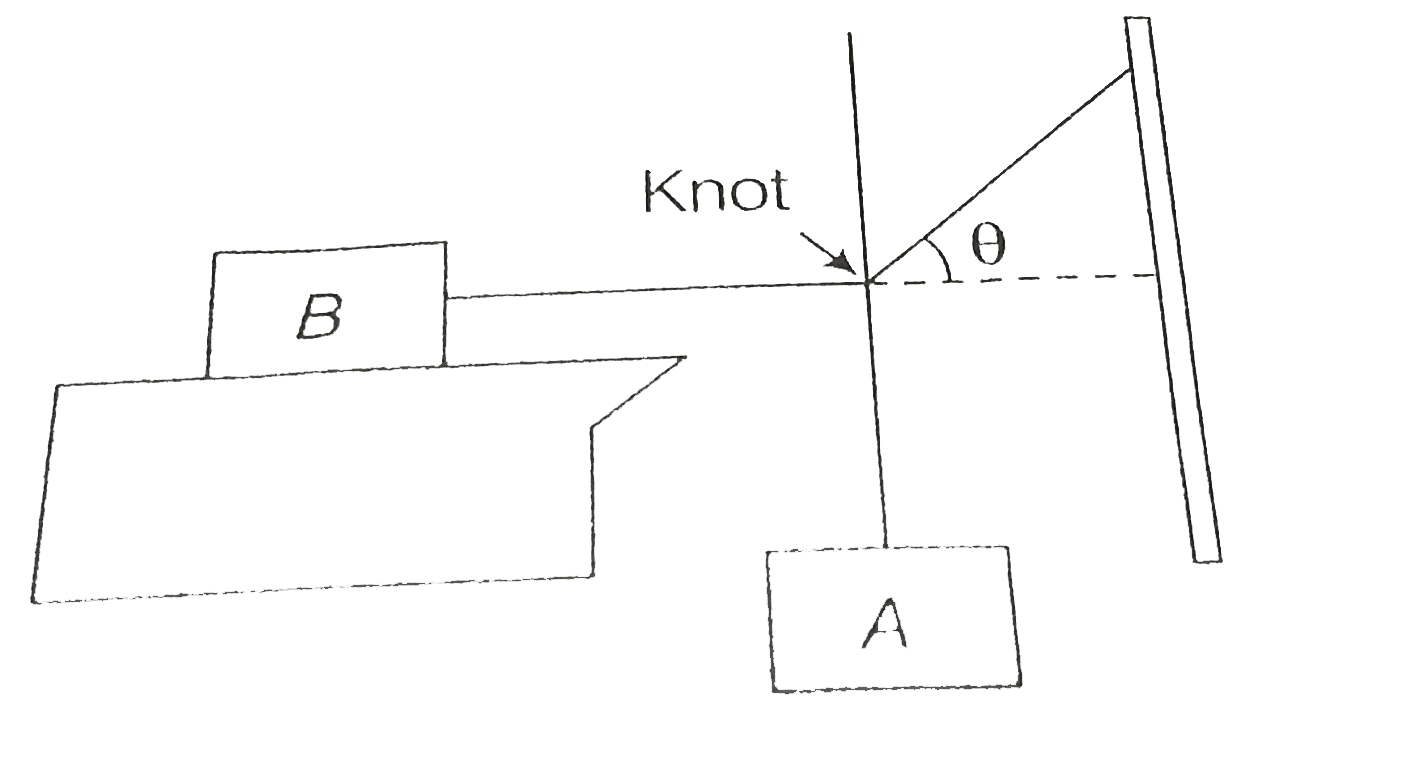 View Solution
View SolutionA 6.00 kg box is sliding across the horizontal floor of an elevator. The coefficient of kinetic friction between the box and the floor is 0.360. Determine the kinetic frictional force that acts on the box when the elevator is stationary.
View SolutionThe coefficient of friction between the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3 m without skidding is (Take g=10ms−2)
View SolutionBlock B lying on a table weighs W. The coefficient of static friction between the block and the table is μ. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
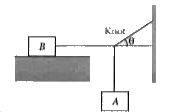 View Solution
View Solution

