Block B lying on a table weighs W. The coefficient of static friction between the block and the table is μ. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
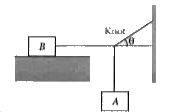
Wtanθμ
μWtanθ
μW√1+tan2θ
μWsinθ
The correct Answer is:B
Weight of block B = W
Weight of block A = W.
T = tension in the string
Normal on block B, N= W
Friction force on block B,f= μN= μW
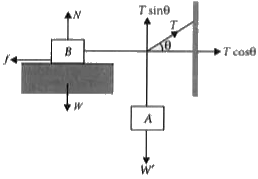
System will be in equilibrium, if
Tcosθ=f=μW ...(i)
Tsinθ=W. ...(ii)
Divide eqn (ii) by eqn (i), we get
sinθcosθ=W.μW,∴W.=μWtanθ
Topper's Solved these Questions
- MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONBOOK - MTG-WBJEECHAPTER - MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONEXERCISE - WB-JEE WORKOUT (CATEGORY 2 : Single Option Correct Type (2 Marks))
25 Videos
- MODEL TEST PAPTER BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPTER EXERCISE - MCQs
80 Videos
- NUCLEAR PHYSICBOOK - MTG-WBJEECHAPTER - NUCLEAR PHYSICEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
5 Videos
Similar Questions
Block B lying on a table weighs w. The coefficient of static friction between the block and the table is mu. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
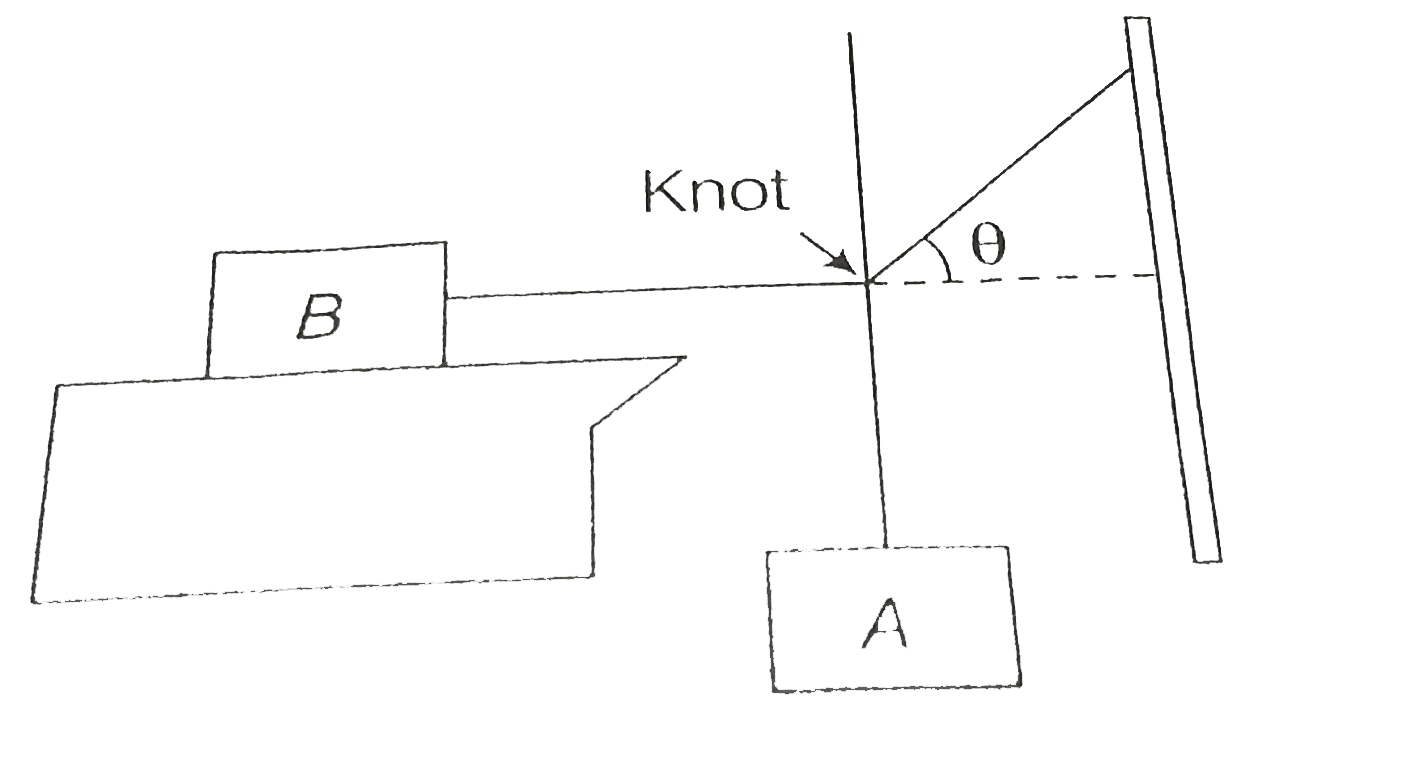
View Solutiona. Block A , as shown in figure weight 60.0N The coefficient of static friction between the block and the surface on which it rest is 0.25 .The system is in equlibrium .Find the friction for excerted on block A
b. Find the maximum weight w for which the system will remain in equlibrium
View Solution
Knowledge Check
Block B lying on a table weighs w. The coefficient of static friction between the block and the table is mu. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
 AwtanθμBμwtanθCμw√1+tan2θDμwsinθ
AwtanθμBμwtanθCμw√1+tan2θDμwsinθA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θThe system shown is just on the verge of slipping. The coefficient of static friction between the block and the table top is :
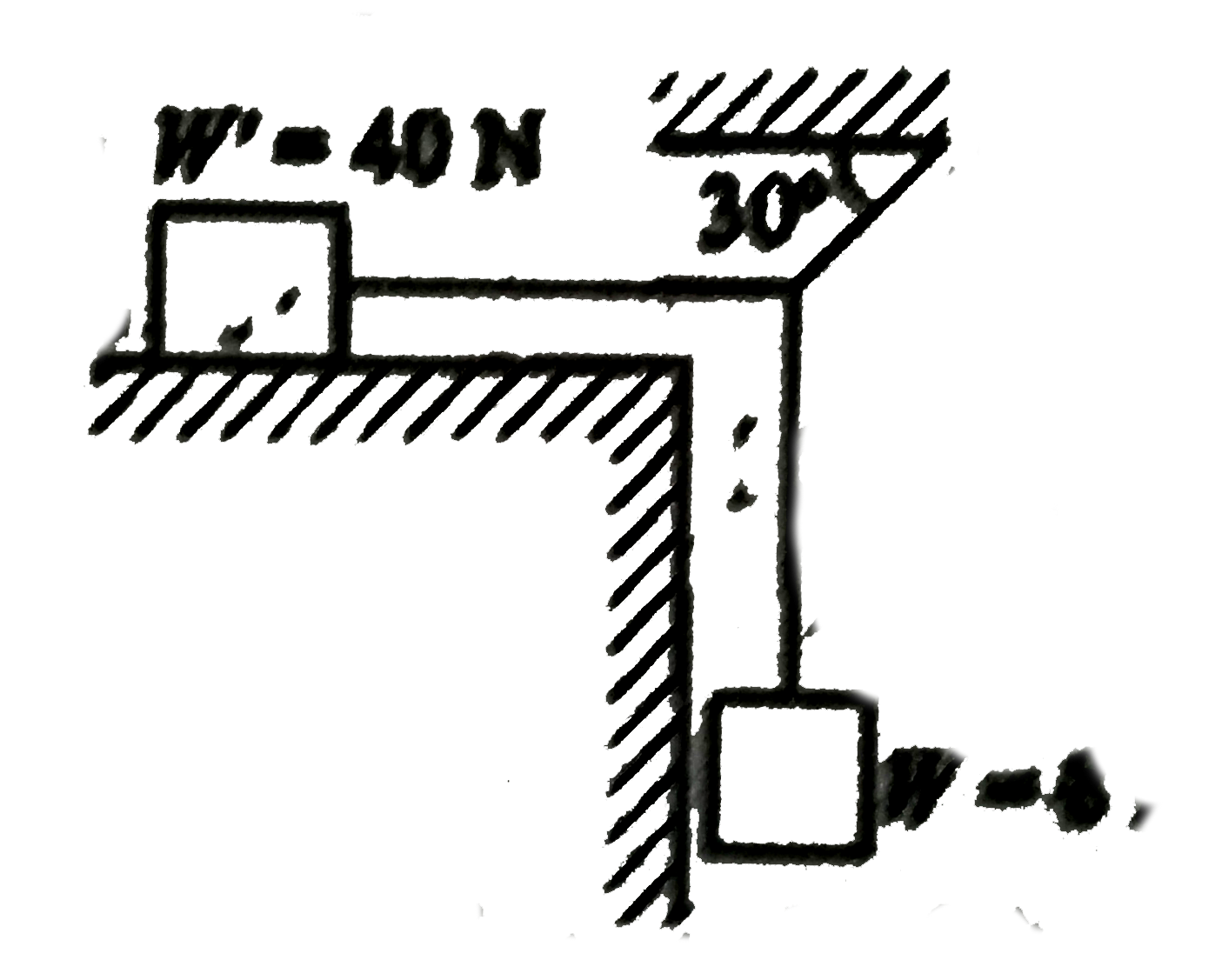 A0.5B0.95C0.15D0.35
A0.5B0.95C0.15D0.35
A block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
 .
.
View SolutionThe coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionA block weighing 10kg is at rest on a horizontal table. The coefficient of static friction between the block and the table is 0.5. If a force acts downward at 60∘ with the horizontal, how large can it be without causing the block to move ? .(g=100ms−2) .
View Solution
