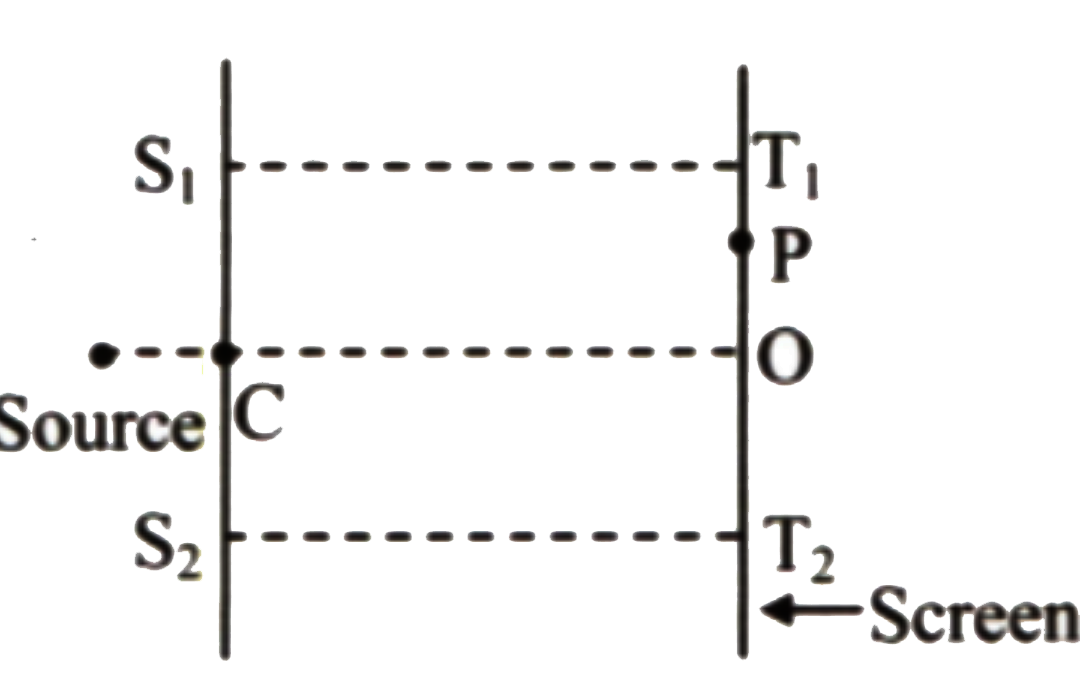
Consider a two slit interference arrangements (figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.

λ2.472
λ2.236
λ1.227
λ3.412
The correct Answer is:A

From diagram
T1P=T1O−OP=(D−x)
T2P=T2O−OP=(D+x)
Now S1P=√(S1T1)2+(T1P)2=√D2+(D−x)2
S2P=√(S2T2)2+(T2P)2=√D2+(D+x)2
Path difference S2P−S1P=λ2, for first minimum to occur
√D2+(D+x)2−√D2+(D−x)2=λ2
The first minimum falls at a distance D from the center, i.e., x=D.
[D2+4D2]1/2−D=λ2
D(√5−1)=λ2
D(2.236−1)=λ2 , D=λ2.472
Topper's Solved these Questions
- WAVE OPTICSBOOK - NCERT FINGERTIPSCHAPTER - WAVE OPTICSEXERCISE - NCERT Exemplar
5 Videos
- WAVE OPTICSBOOK - NCERT FINGERTIPSCHAPTER - WAVE OPTICSEXERCISE - Assertion And Reason
15 Videos
- WAVE OPTICSBOOK - NCERT FINGERTIPSCHAPTER - WAVE OPTICSEXERCISE - Polarisation
18 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTIPSCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
In a special arrangement of Young's double - slits d is twice the distance between the screen and the slits D, i.e. d = 2D. For the setup, the value of D such that the first minima on the screen fall at a distance D from the centre O is found to be λN, where λ is the wavelength of light used. What is the value of N ? [Take √5=2.24]
View SolutionIn a special arrangement of Young's double - slits d is twice the distance between the screen and the slits D, i.e. d = 2D. For the setup, the value of D such that the first minima on the screen fall at a distance D from the centre O is found to be λN, where λ is the wavelength of light used. What is the value of N ? [Take √5=2.24]

View Solution
Knowledge Check
In a YDSE arrangement, the distance of screen from the slits is half the distance between the slits. If 'λ' is the wavelength of then the value of D such that first minima on the screen falls at a distance D from then centre 'O' is
 AD=λ√5BD=λ2CD=λ5√2DD=λ2√5
AD=λ√5BD=λ2CD=λ5√2DD=λ2√5In young's double slit experiment, if the distance between the slits is halved and the distance between the slits and the screen is doubled, the fringe width becomes
AunchangedBhalvedCdoubledDquadrupledIn Young's experiment the distance between the slits is reduced to half and the distance between the slit and screen is doubled then the fringe width
Awill not changeBwill become halfCwill be doubledDwill become four times
The distance between two slits in a YDSE apparatus is 3mm. The distance of the screen from the slits is 1m. Microwaves of wavelength 1 mm are incident on the plane of the slits normally. Find the distance of the first maxima on the screen from the central maxima.
View SolutionThe distance between two slits in a YDSE apparatus is 3mm. The distance of the screen from the slits is 1m. Microwaves of wavelength 1 mm are incident on the plane of the slits normally. Find the distance of the first maxima on the screen from the central maxima.
View SolutionIn Young's experiment, the distance between the slits is 0.025 cm and the distance of the screen from the slits is 100 cm. If two distance between their second maxima in cm is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View Solution
