Question

In a special arrangement of Young's double - slits d is twice the distance between the screen and the slits D, i.e. d = 2D. For the setup, the value of D such that the first minima on the screen fall at a distance D from the centre O is found to be $\frac{\lambda }{N}$, where $\lambda$ is the wavelength of light used. What is the value of N ? $[\text{Take}\sqrt{5}=2.24]$

Answer

2.48

Explanation

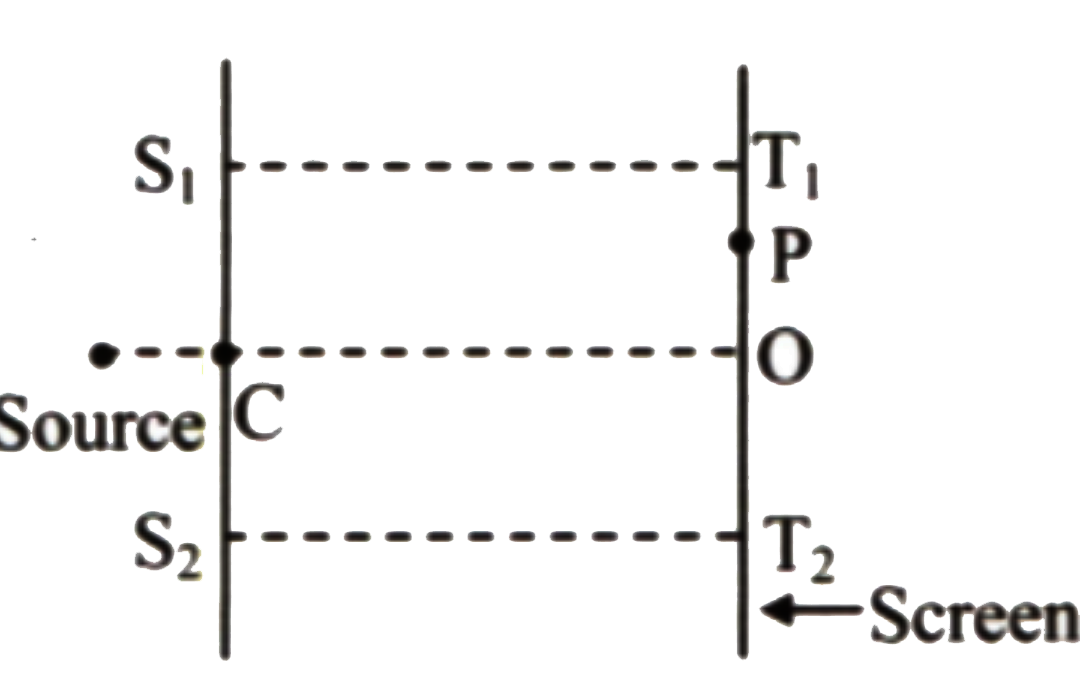
From diagram as provided in question,
OP =x
CO =D
`S_(1) C = S_(2) C =D `
`T_(1) P = T_(1) O - OP =D -x `
`T_(2) P = T_(2) O + OP =D +x `
Now `S_(1)p = sqrt((S_(1)T_(1))^(2)+(T_(1)P)^(2))`
`=sqrt(D^(2)+(D-x)^(2))`
`S_(2) P = sqrt((S_(2)T_(2))^(2) + (T_(2)P)^(2))`
`= sqrt(D^(2) +(D+x)^(2))`
For fist minimum to occur, Path difference
`S_(2) P - S_(1) P = (lambda)/(2)`
`implies sqrt(D^(2) +(D+x)^(2))`
`- sqrt(D^(2)+(D-x))^(2)=(lambda)/(2)`
The first minimum falls at a distance D from the centre, i.e., x = D
`[D^(2) +4D^(2) ]^((1)/(2))-D=(lambda)/(2)`
`:. D (sqrt(5)-1)=(lambda)/(2)`
`implies D = (lambda)/(2(2.24-1))=(lambda)/(2.48)`
Hence, the required value of N = 2. 48