The give figure shows a square ABCD and an equilayeral teiangle APB. Calculate :
(1)∠AOB(ii)∠BPC(iii)∠PCD(iv)reflex∠APC
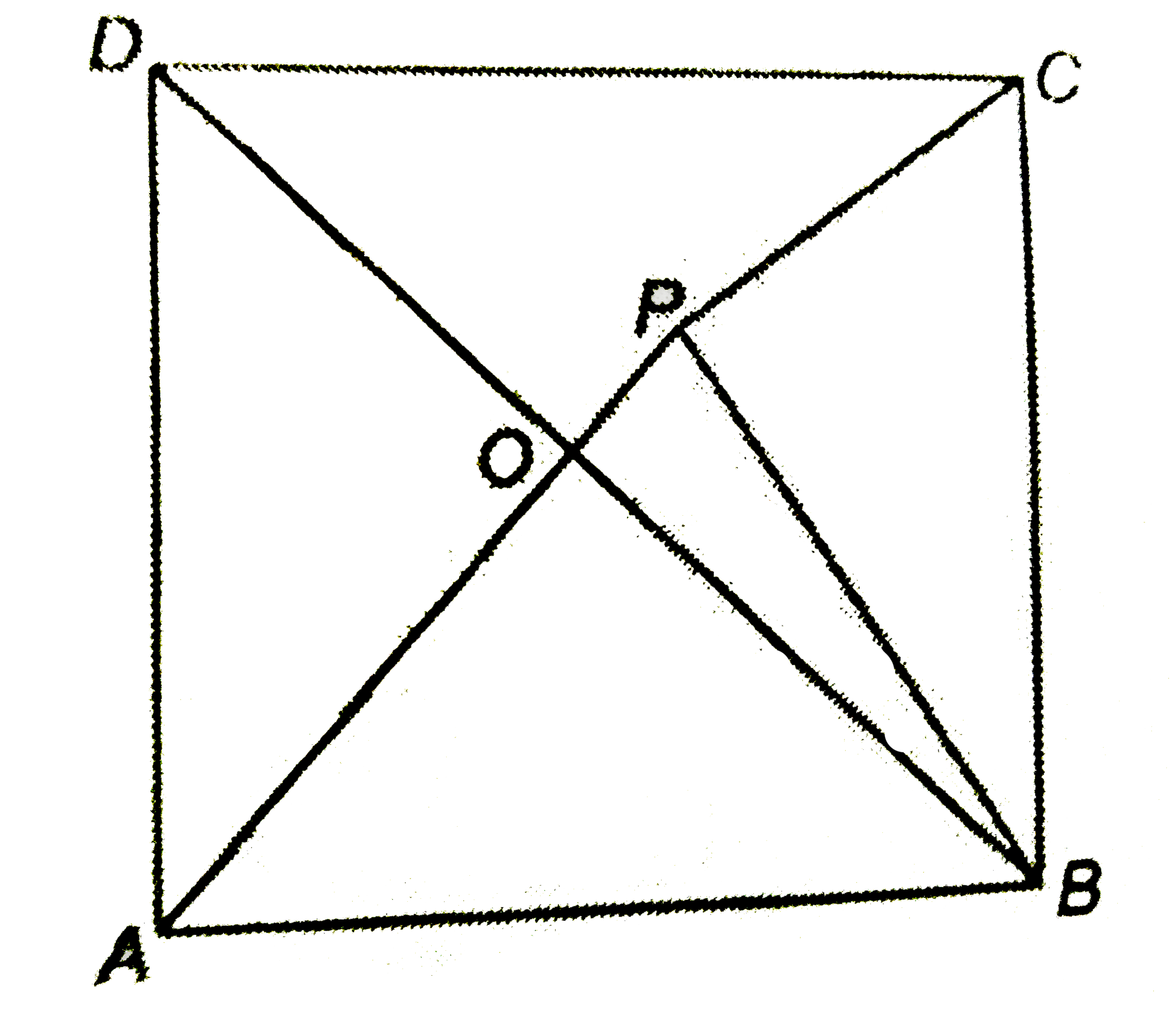
(i)75∘ (ii)75∘ (ii)15∘ (iv)225∘
(i)55∘ (ii)65∘ (ii)35∘ (iv)215∘
(i)65∘ (ii)35∘ (ii)45∘ (iv)220∘
(i)45∘ (ii)65∘ (ii)35∘ (iv)125∘
The correct Answer is:A
Step by step video, text & image solution for The give figure shows a square ABCD and an equilayeral teiangle APB. Calculate : {:((1)angleAOB,(ii)angleBPC),((iii)anglePCD,(iv)"reflex"angleAPC):} by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b15videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)10videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise10videos
STATISTICS
Similar Questions
The given figure shows a square ABCD and an equilateral triangle ABP Calculate
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP Calculate:
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate: ∠AOB,∠BPC
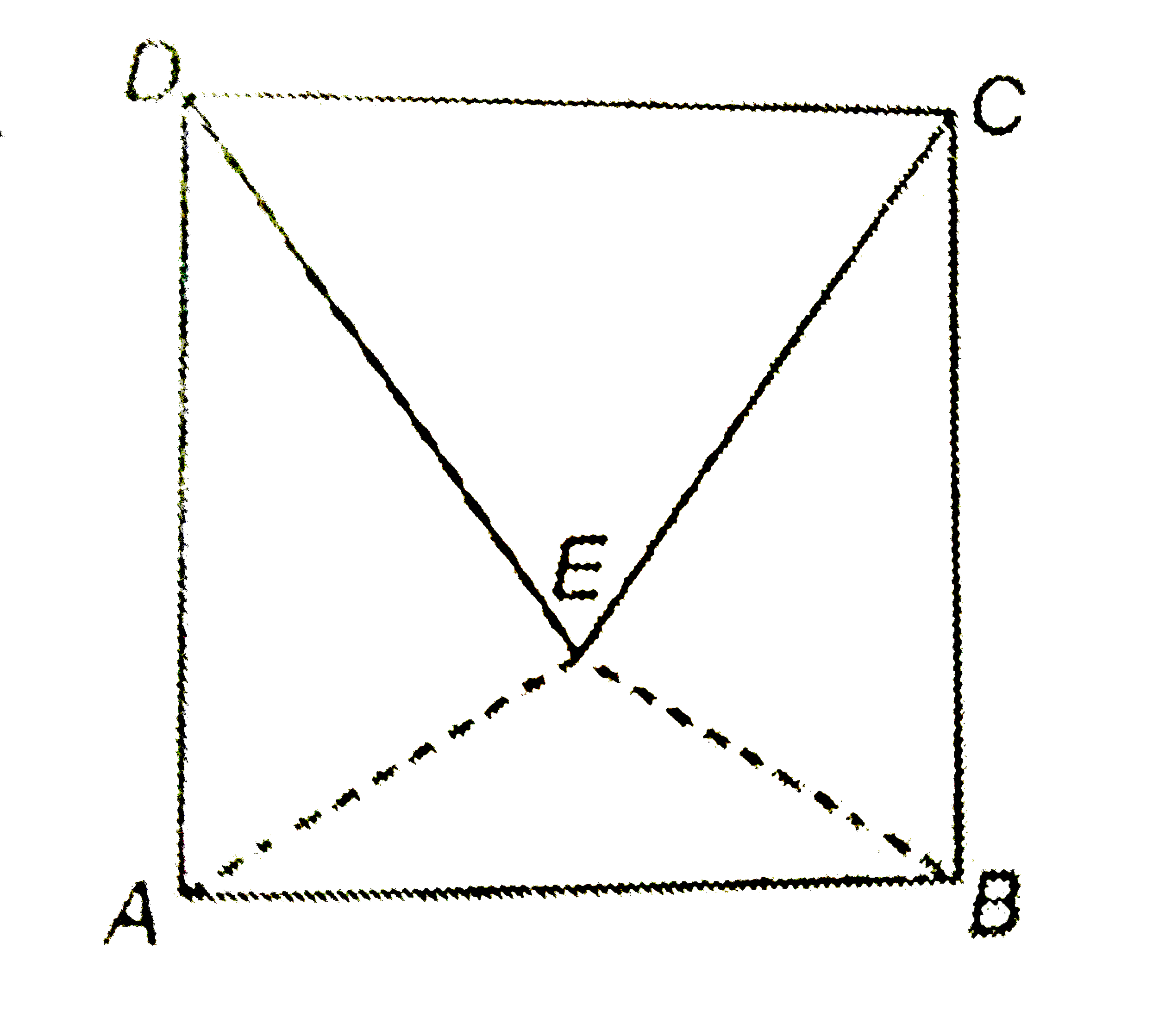
View SolutionThe adjoining figure shows a square ABCD and an equilateral triangle DEC. Prove that :
(i) ∠ADE=∠BCE=30∘
(ii) Δ≅ΔBCE
 View Solution
View SolutionThe following figure shows a square ABCD and an equilateral triangle DCE. Prove that :
(i) ∠ADE=∠BCE=150∘
(ii) ΔADE≅ΔBCE
(iii) AE=BE
 View Solution
View SolutionIn the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP
 View Solution
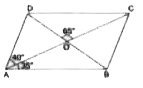
View SolutionIn the adjoining figure , ABCD is a parallelogram in which ∠CAD=40∘,∠BAC=35∘ and ∠COD=65∘ Calculate : (i)∠ABD (ii)∠BDC (iii)∠ACB (iv) ∠CBD
 View Solution
View Solution\n the following diagrams, ABCD is a square and APB is an equilateral triangle.In each case ,(1) Prove that : △ APD = △ BPC (ii) Find the angles of △ DPC.
View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)
 View Solution
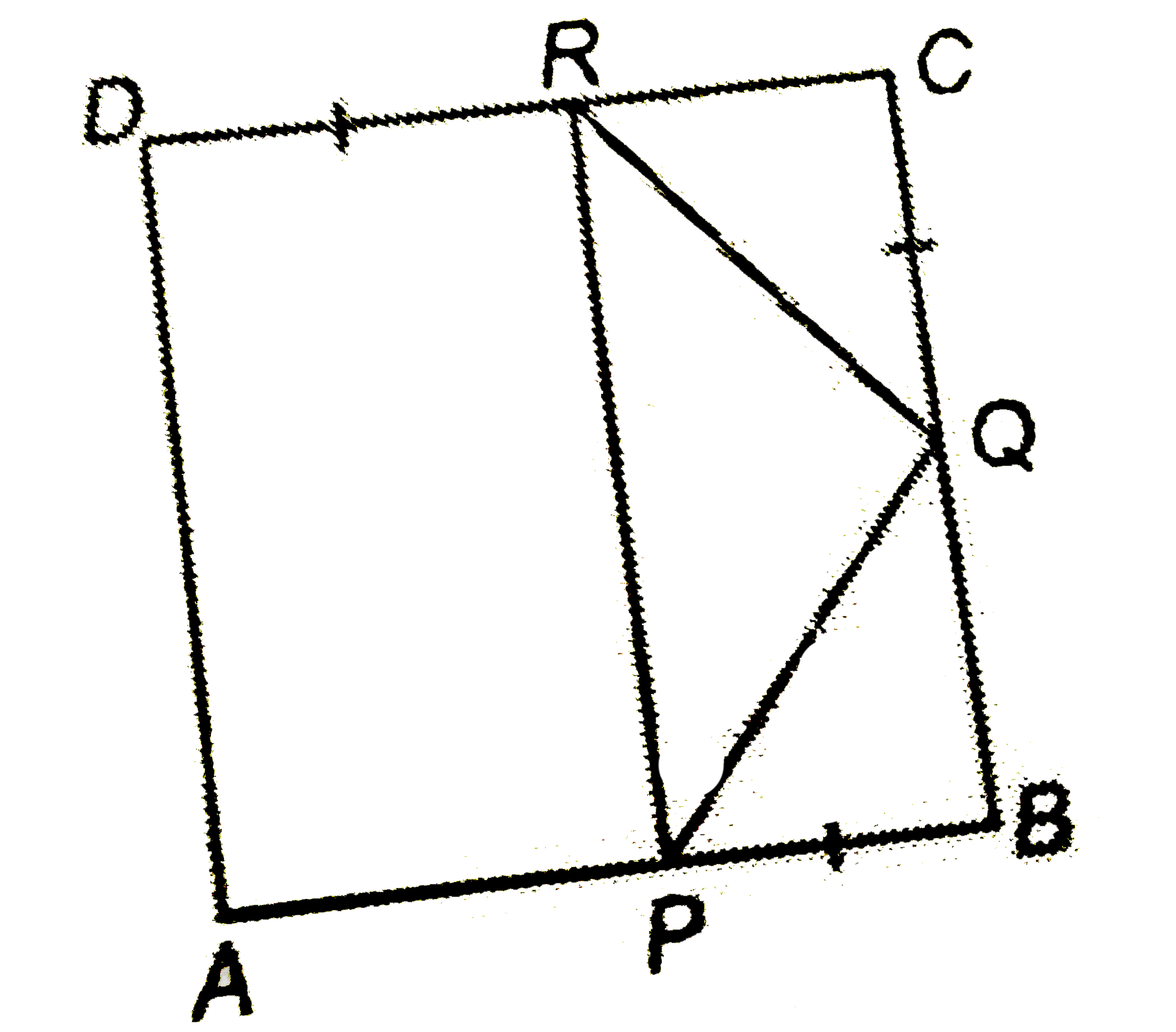
View SolutionIn the given figure, ABCD is a square and ∠PQR=90∘.IfPB=QC=DR, prove that.
(i) QB = RC
(ii) PQ = QR
(iii) ∠QPR=45∘
 View Solution
View Solution

