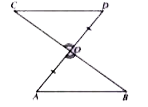
In a square ABCD, diagonals meet at O. P is point on BC such that OB = BP.Show that (i) ∠POC=(2212)∘
(ii) ∠BDC=2∠POC
(iii) ∠BOP=3∠COP
Step by step video, text & image solution for In a square ABCD, diagonals meet at O. P is point on BC such that OB = BP.Show that (i) anglePOC=(22(1)/(2))^(@) (ii) angleBDC=2anglePOC (iii) angleBOP=3angleCOP by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
Knowledge Check
In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
Ax - y - 1 = 0Bx + y - 1 = 0Cx - y + 1 = 0Dx + y - 7 =0Let ABCD be a square and let P be a point on AB such that AP:PB=1:2.if∠APD=θ, then what is the value of cosθ?
A1√10B1√5C2√10D2√5
ABCD is a trapezium in which AB∣∣CD and AD=BC. Show that
(i)∠A=∠B
(ii) ∠C=∠D
(iii) △ABC≅=△BAD
(iv) diagonal AC=diagonal BD

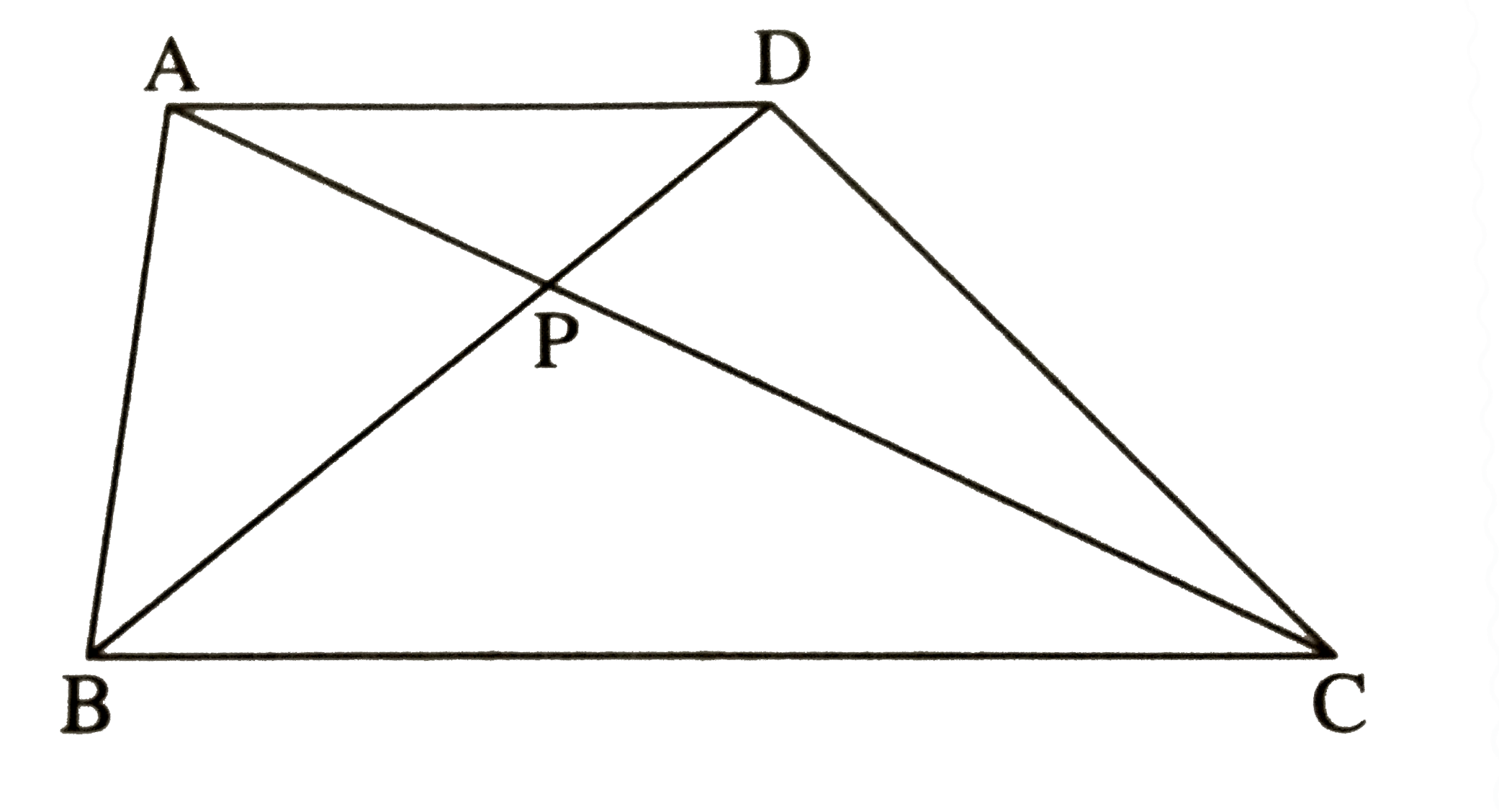
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.

View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

View SolutionIn Figure, RENT is a rectangle. Its diagonals meet at O. Find x, if OR=2x+4 and OT=3x+1.
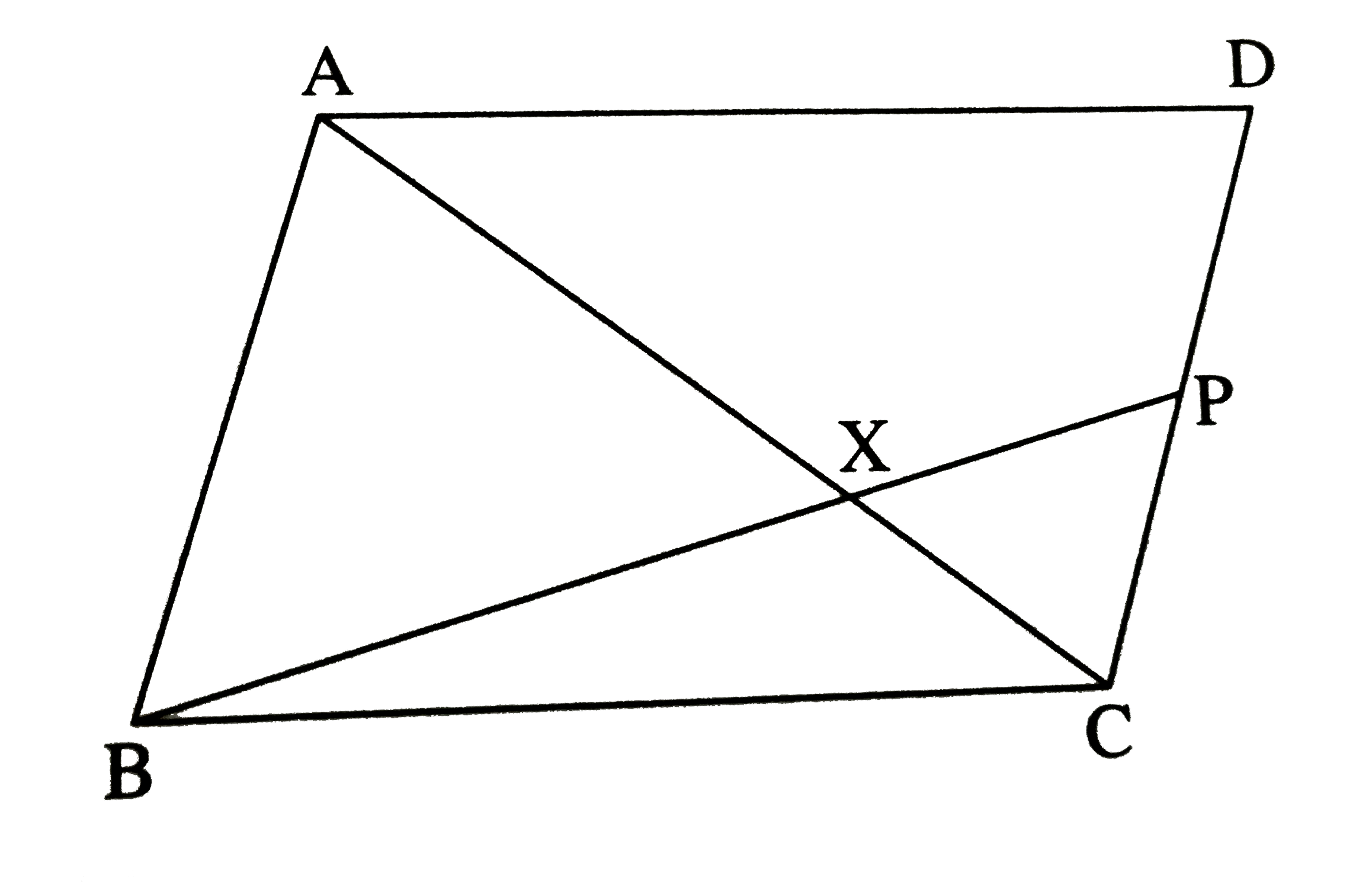
View Solution□ABCD is a parallelogram. P is the midpoint of side CD. Seg BP meets diagonal AC at X. Prove that 3AX=2AC.
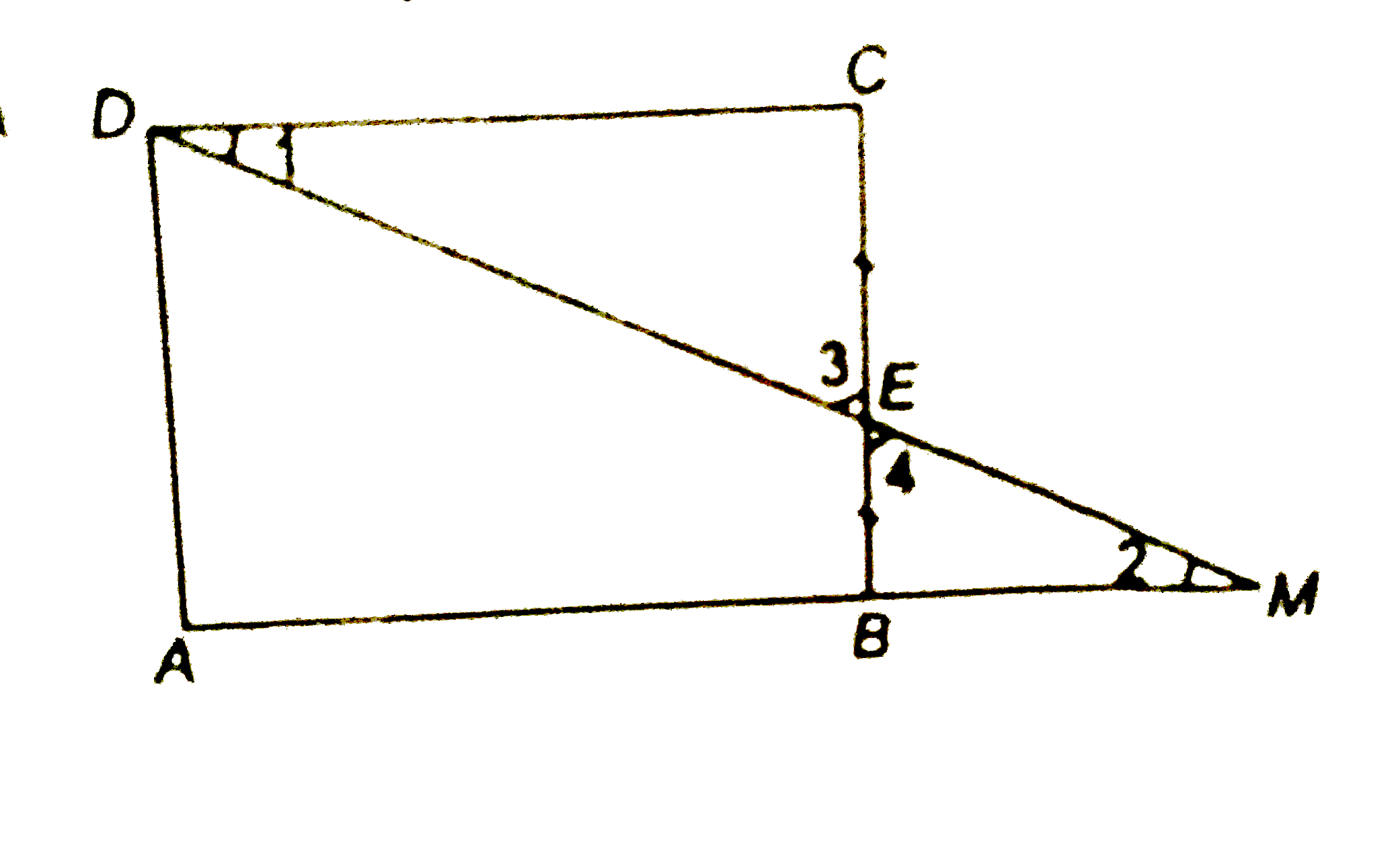
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
View Solution