The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table.

the rate equation for the reaction is : r=k[A]1[B]0
i) Comparing experiments I and II.
2.0×10−2=k[0.1]1[0.1]0
4.0×10−2=k[x]1[0.2]0
Dividing eqn.(ii) by eqn. (i),
4.0×10−22.0×10−2=k[x]1[0.2]0k[0.1]1[0.1]0,2=x0.1orx=2×0.1=0.2M
Thus, concentration of A in experiment II is 0.2 M
ii) Comparing experiments II and III.
When the concentration of A is made double, the reaction rate will also becomes twice.
∴ Rate of reaction in experiment III is 8.0×10−2
iii) Comparing experiments I and IV,
Since, the reaction rates are the same in both the experiments, the molar concentration of A in experiment IV must be the same as in experiment I. i.e., it must be 0.1 M.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Short Answer type questions
20 Videos
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Additional important questions:
16 Videos
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - NCERT Exercise
1 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Unit Test - 1
20 Videos
- CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS BOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS EXERCISE - Exercise
507 Videos
Similar Questions
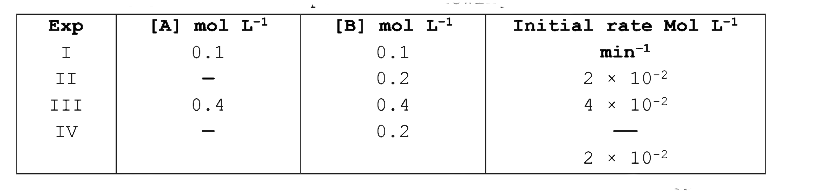
The reaction between A and B is first order with respect to A and zero with respect to B. Fill in tha blanks in the following table:
Experiment[A]/M[B]/MInitial rate/M minI.0.10.12.0×10−2II.....0.24.0×10−2II.0.40.4.......IV.....0.22.0×10−2
View SolutionThe reaction between A and B is 1st order w.r.t to A and zero order w.r.t B. Find the value of [A] and rate as per the following blanks
View Solution
Knowledge Check
The reaction between X and Y is first order with respect to X and second order with respect to Y. If the concentration of X is halved and the concentration of Y is doubled, the rate of reaction will be
Athe same as the initial valueBthree times the initial valueCdouble the initial valueDhalf the initial value.The reaction between X and Y is first order with respect to X and second order with respect to Y. If the concentration of X is halved and the concentration of Y is doubled, the rate of reaction will be
Athe same as the initial valueBthree times the initial valueCdouble the initial valueDhalf the initial value.The reaction between X and Y is first order with respect to X and second order with respect to Y. If the concentration of X is halved and the concentration of Y is doubled, the rate of reaction will be
Athe same as the initial valueBthree times the initial valueCdouble the initial valueDhalf the initial value.
Fill in the blanks in the following table which treats a reaction of a compound A with a compound B, that is the first order with respect to A and zero order with respect to B.

View SolutionFill in the balanks in the following table which treats reaction of a compound A with a compound B , that is of the first order with respect to A and zero order with respect to B :
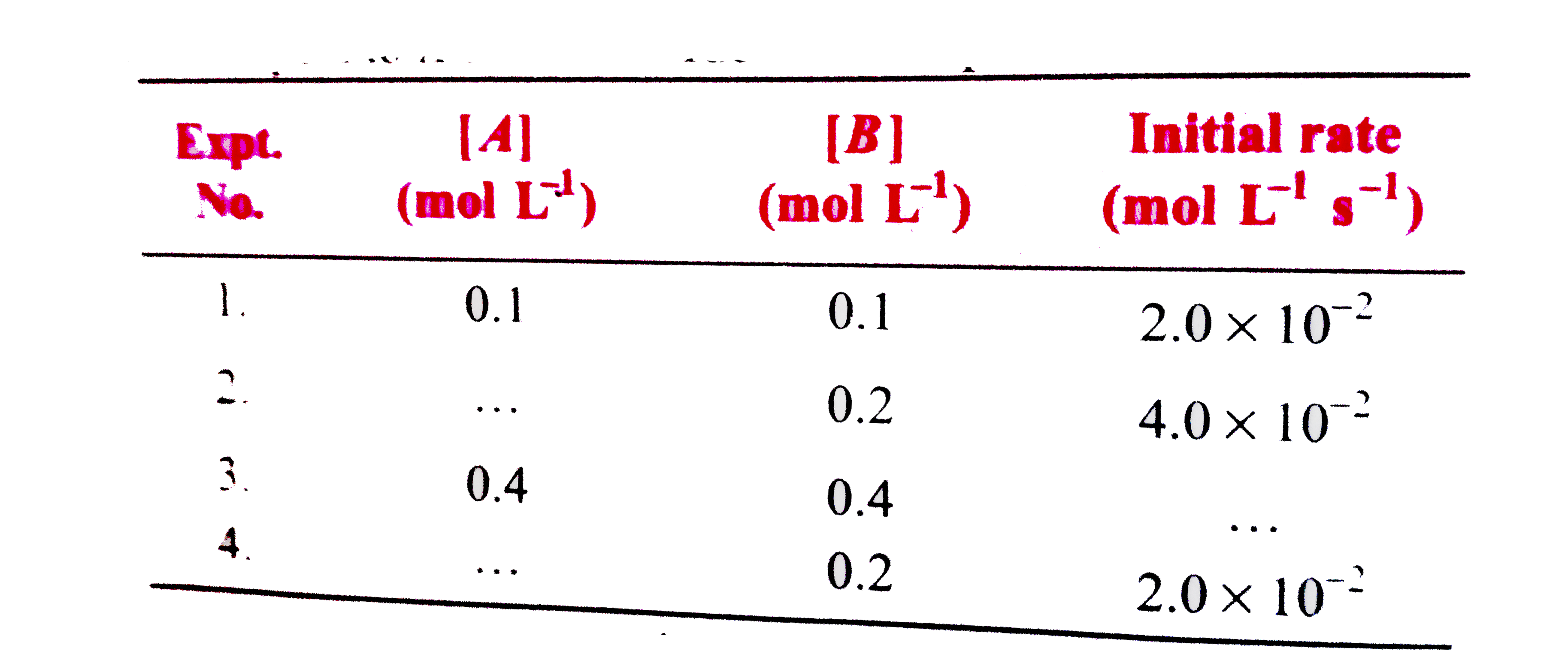
View SolutionThe reaction v1A+v2B→ products is first order with respect to A and zero-order with respect to B. If the reaction is started with [A0]and[B0], then the integrated rate expression of this reaction would be:
View SolutionFor the raction A+B→ products, it is found that order of A is 2 and the order of B is 3. In the rate expression when the concentration of both A and B are doubled the rate will increases by a factor
View SolutionA reaction of first order with respect to reactant A and second order with respect to reactant B. the rate law for the reaction is given by
View Solution
