The rate constant for the first order decomposition of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life period be 256min?
Step I. Calculation of activation energy (Ea)
According to Arrhenius equation , k=Ae−Ea/RT.
log k =logA−Ea2.303RT
The given equ. Is log k =14.34−1.25×104(K)T
On comparison: Ea2.303RT=1.25×104(K)T
Ea=1.25×104×2.303×8.314(Jmol−1)
=239,339Jmol−1=239.339kJmol−1
Step II. Calculation of desired temperature
For the first order reaction , k =0.693t1/2=0.693256min=0.693256×60s=4.51×10−5s−1
According to Arrheneius theory, log k =14.34−1.25×104T , −4.35=14.34−1.25×10418.69=669K
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Short Answer type questions
20 Videos
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Additional important questions:
16 Videos
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - NCERT Exercise
1 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Unit Test - 1
20 Videos
- CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS BOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS EXERCISE - Exercise
507 Videos
Similar Questions
The rate constant for the first order decompoistion of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be 256min?
View SolutionThe rate constant for the first order decompoistion of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be 256min?
View Solution
Knowledge Check
The rate constant for the decompoistion of a certain reaction is described by the equation:
logk(s−1)=14−1.25×104KT
Energy of activation (in kcal) isA57.6kcalB1.25×104kcalC14.0kcalD14×104kcalThe rate constant for the decompoistion of a certain reaction is described by the equation:
logk(s−1)=14−1.25×104KT
Pre-exponential factor for this reaction isA14s−1B1014s−1C10−14s−1D1.25×104s−1The rate constant for the decompoistion of a certain reaction is described by the equation:
logk(s−1)=14−1.25×104KT
At what temperature, rate constant is equal to pre-exponential factor?AT=1.25×104K14BT=∞CT=0D(14−1.25×104)K
Rate constant for the decomposition of ethylene oxide into CH4 and CO may be described by the equation logl(s−1)=14.34−1.25×104T
(a) What is the energy of activation of this reaction ?
(b) What is the value of k at 670K ?
View SolutionRate constant for the decomposition of ethylene oxide into CH4 and CO may be described be the equation. logk(s)−1=14.34−1.25×104T
(a) What is the energy of activation of this reaction ?
(b) What is the value of k at 670K ?
View SolutionThe rate constant of the first order reaction , that is decomposition of ethylene oxide into CH4 and CO, may be described by the following equation
logk(s−1)=14.34−1.25×104TK
Find (a) energy of activation ,
View SolutionThe rate constant for the first order decomposition of ethylene oxide into CH4 and CO,
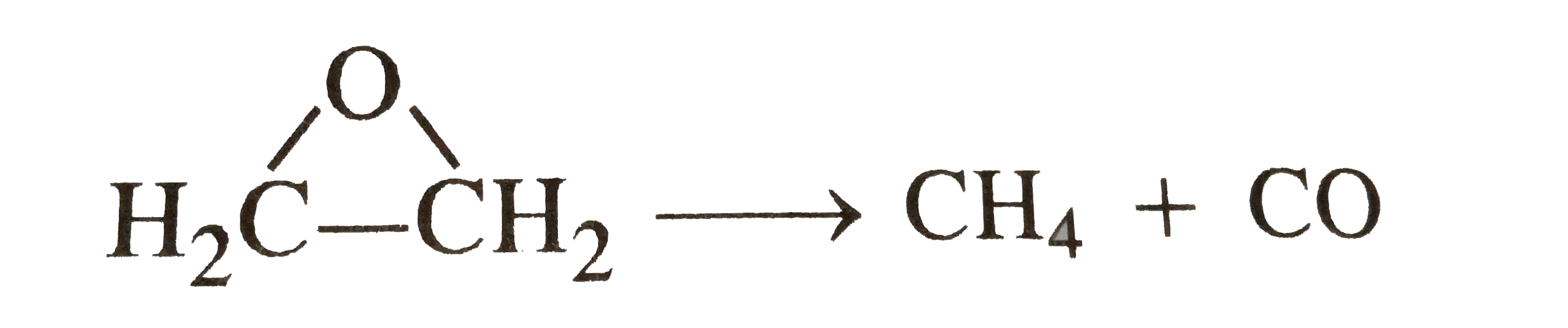
may be describe by
logk(ins−1)=14.34−1.25×104KT
The activation energy of the reaction is
View SolutionThe rate constant for the decompoistion of a certain reaction is described by the equation:
logk(s−1)=14−1.25×104KT
What is the effect on the rate of reaction at 127∘C, if in the presence of catalyst, energy of activation is lowered by 10kJmol−1?
View Solution
