A vector has a magnitude x . If it is rotated by an angle θ then magnitude of change in vector is nx. Match the following two columns.
Column I Column II(A)θ=60∘(P)n=√3(B)θ=90∘(Q)n=1(C)θ=120∘(r)n=√2(D)θ=180∘(s)n=2
The correct Answer is:A→q, B→r , C→ p, D→s
(a)When θ=60∘

(b) When θ=90∘

( c)When θ=120∘
∴n=√3

(d)When θ=180∘

Topper's Solved these Questions
Similar Questions
A vector of magnitude b is rotated through angle θ. What is the change in magnitude of the vector?
View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
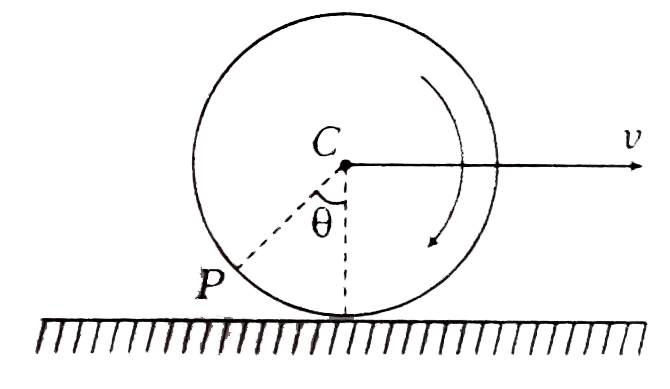
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3vView Solution
Knowledge Check
- Question 1 - Select One
If θ is the angle between two vectors A and B , then match the following two columns.
Column I Column II(A)A.B=|A×B|(P)θ=90∘(B)A.B=B2(Q)θ=0∘or180∘(C)|A+B|=|A−C|(r)A=B(D)|A×B|=AB(s)NoneAA→s, B→q,r , C→p, D→pBA→p, B→q,r , C→p, D→sCA→s, B→q,r , C→s, D→pDA→s, B→q , C→r, D→p - Question 2 - Select One
The correct match of the following is :
Column - IColumn - II(i)nCr(a)n!(ii)nC0(b)1(iii)nPr(c)r!.nCr(iv)nPn(d)nCn−rA(i)-(d), (ii)-(b), (iii)-(c ), (iv)-(a)B(i)-(a), (ii)-(b), (iii)-(c ), (iv)-(d)C(i)-(b), (ii)-(c ), (iii)-(d), (iv)-(a)D(i)-(d), (ii)-(b), (iii)-(a), (iv)-(c ) - Question 3 - Select One
Two vectors inclined at an angle θ have magnitude 3N and 5N and their resultant is of magnitude 4N. The angle θ is
A90∘Bcos−1(45)Ccos−1(35)Dcos−1(−35)
Match the column:

∣∣ ∣ ∣ ∣ ∣ ∣∣Column -1Column -2(A)θ=37∘(P)f is upwards(B)θ=45∘(Q)f is downwards(C)θ=53∘(R)f is static(S)f is kinetic∣∣ ∣ ∣ ∣ ∣ ∣∣View SolutionA pendulum is released from point A as shown in figure. At some instant net force on the bob is making and angle θ with the string. Then match the following:

Column-1 Column-2(A)Forθ=30∘(P) Particle may be moving between B & A(B)Forθ=120∘(Q) Particle may be moving between C & B particle is at A(C)Forθ=90∘(R) Particle is at A(D)Forθ=0∘(S) Particle is at B(T) NoneView SolutionIf secθ=m+n2√mnfind sinθ
View SolutionIf tanpθ=cotqθ, then θ=2n+12(p+q)π
View SolutionFor 0<θ<π4, let x=∞∑n=0sin2nθ,y=∞∑n=0cos2nθ, then match the entries of column-I with column-II
Column-IColumn-II(a)∑∞0sin2nθcos2nθ(p)xy2xy2−1(b)∑∞0tan2nθ(q)yy−x(c)∑∞0sin2nθcos4nθ(r)xyxy−1(d)∑∞0cos2nθsin4nθ(s)x2yx2y−1View Solution

