If θ is the abgle between two vectors A and B , then match the following two columns.
Column I Column II(A)A.B=|A×B|(P)θ=90∘(B)A.B=B2(Q)θ=0∘or180∘(C)|A+B|=|A−C|(r)A=B(D)|A×B|=AB(s)None
A→s, B→q,r , C→p, D→p
A→p, B→q,r , C→p, D→s
A→s, B→q,r , C→s, D→p
A→s, B→q , C→r, D→p
The correct Answer is:A
Step by step video, text & image solution for If theta is the abgle between two vectors A and B , then match the following two columns. {:(,"Column I ",,"Column II"),((A),A.B=|AxxB|,(P),theta=90^(@)),((B),A.B=B^(2),(Q),theta=0^(@)or 180^(@)),((C),|A+B|=|A-C|,(r),A=B),((D), |AxxB|=AB,(s),"None"):} by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Two vector A and B have rqual magnitude x .Angle between tjem is 60∘ Then match the following two columns.
Column I Column II(A)|A+B|(P)√32x2(B)|A−B|(Q)x(C)A.B(r)√3x(D)|A×B|(s)NoneView SolutionVector A is pointing eastwards and vector B northwards .If |A|=|B| then match the following two columns.
Column I Column II(A)(A+B)(P)north -east(B)(A−B)(Q)Vertically upwards(C)(A×B)(r)Vertically downwads(D)(A×B)×(A×B)(s)NoneView Solution
Knowledge Check
- Question 1 - Select One
θ is the angle between two vectors a and b then a.b≤0 only if
A0≤θ≤πBπ/2≤θ≤πC0≤θ≤π/2D0<θ<π/2 - Question 2 - Select One
If θ is the angle between vectors a and b, then |a×b|=|a.b|, then θ is equal to
A0B180∘C135∘D45∘ - Question 3 - Select One
If θ is the angle between vectors a and b, then |a×b|=|a.b|, then θ is equal to
A0B180∘C135∘D45∘
A vector has a magnitude x . If it is rotated by an angle θ then magnitude of change in vector is nx. Match the following two columns.
Column I Column II(A)θ=60∘(P)n=√3(B)θ=90∘(Q)n=1(C)θ=120∘(r)n=√2(D)θ=180∘(s)n=2View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
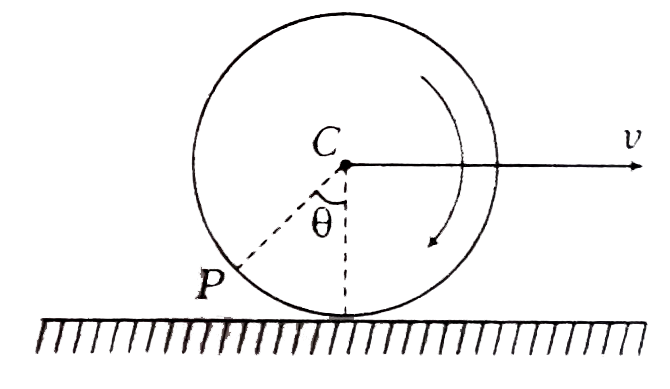
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3vView SolutionGiven θ be the angle between unit vectors A and B Then, |AxxB| is equal to
View SolutionIf θ is the angle between vectors a and b and |a×b|=|a.b| then θ is equal to
View SolutionIf A.B=A×B, then angle between A and B is
View Solution

