A point traversed 3/4 th of the circle of radius R in time t. The magnitude of the average velocity of the particle in this time interval is
πRt
3πR2t
R√2t
R√2t
The correct Answer is:C
To find the magnitude of the average velocity of a particle that traverses 3/4 of a circle of radius R in time t, we can follow these steps:
Step 1: Understand the Motion
The particle travels along a circular path and covers 3/4 of the circumference of the circle. The initial position and final position of the particle will help us determine the displacement.
Step 2: Determine the Displacement
The displacement is defined as the straight-line distance between the initial and final positions of the particle.
- The initial position can be considered at point A (0 degrees) on the circle.
- After traversing 3/4 of the circle, the particle reaches point B (270 degrees).
Step 3: Visualize the Geometry
In a circle of radius R:
- The coordinates of point A (initial position) are (R, 0).
- The coordinates of point B (final position) are (0, -R).
Step 4: Calculate the Displacement
The displacement vector can be calculated using the distance formula between points A and B:
Displacement=√(xB−xA)2+(yB−yA)2
Substituting the coordinates:
Displacement=√(0−R)2+(−R−0)2=√R2+R2=√2R2=R√2
Step 5: Calculate the Average Velocity
The average velocity is defined as the total displacement divided by the total time taken:
Average Velocity=DisplacementTime=R√2t
Final Answer
Thus, the magnitude of the average velocity of the particle in this time interval is:
R√2t
The particle travels along a circular path and covers 3/4 of the circumference of the circle. The initial position and final position of the particle will help us determine the displacement.
The displacement is defined as the straight-line distance between the initial and final positions of the particle.
- After traversing 3/4 of the circle, the particle reaches point B (270 degrees).
In a circle of radius R:
- The coordinates of point A (initial position) are (R, 0).
- The coordinates of point B (final position) are (0, -R).
The displacement vector can be calculated using the distance formula between points A and B:
Displacement=√(0−R)2+(−R−0)2=√R2+R2=√2R2=R√2
The average velocity is defined as the total displacement divided by the total time taken:
Thus, the magnitude of the average velocity of the particle in this time interval is:
Topper's Solved these Questions
- MOTION IN A PLANEBook:DC PANDEYChapter:MOTION IN A PLANEExercise:Check point 3.3
Explore 10 Videos
- MOTION IN A PLANEBook:DC PANDEYChapter:MOTION IN A PLANEExercise:Check point 3.4
Explore 15 Videos
- MOTION IN A PLANEBook:DC PANDEYChapter:MOTION IN A PLANEExercise:Check point 3.1
Explore 10 Videos
- MOTIONBook:DC PANDEYChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- PROJECTILE MOTIONBook:DC PANDEYChapter:PROJECTILE MOTIONExercise:Level - 2 Subjective
Explore 10 Videos
Similar Questions
A particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View SolutionFigure shows the velocity time graph for a particle travelling along a straight line. The magnitude of average velocity (in m/s) of particle during the time interval from t=0 to t=6s is 10α. Find the value of α.
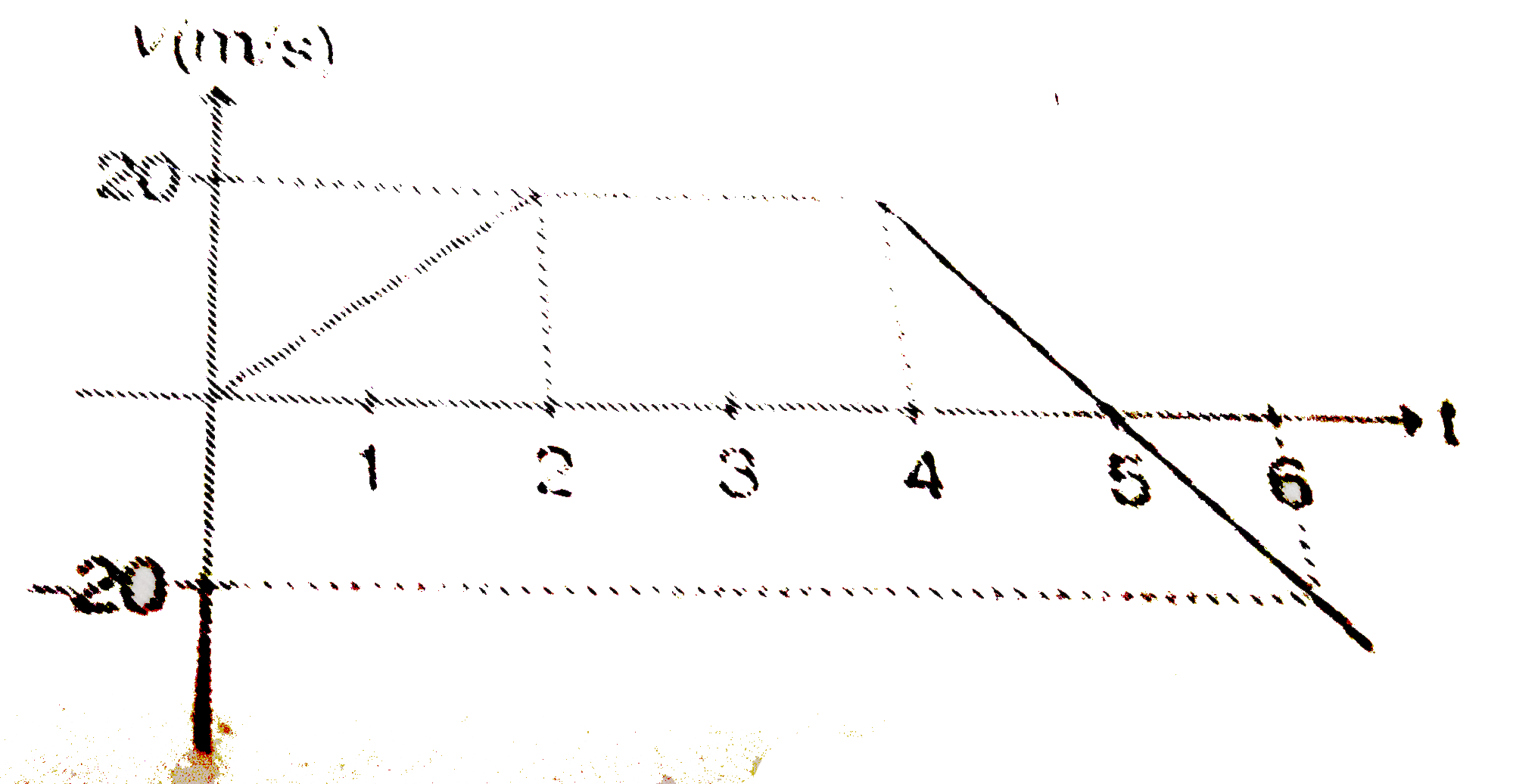
View Solution
Knowledge Check
A particle travels two and a half revolutions of the circle of radius R in time t. The ratio of the average speed of the particle to the magnitude of the average velocity in this time interval is
Aπ2B5π√2C5π2Dπ5√2Starting from rest, a particle rotates in a circle of radius R 2 m with an angular acceleration = /4 rad/s2.The magnitude of average velocity of the particle over the time it rotates quarter circle is:
A1.5m/sB2m/sC1m/sD1.25m/sA point traversed half a circle of radius r during a time interval t0, its mean speed and magnitude of mean velocity are
Aπrt0,rt0B2πrt0,2rt0Cπrt0,2rt0D2πrt0,rt0
A particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View SolutionA particle moves in a straight line. Figure-1.21 shows the distance traversed by the particle as a function of time t.Using the graph, find (a)the average velocity of the point during the time of motion, (b) the maximum velocity, (c) the time t=t0 at which the instantaneous velocity is equal to the mean velocity averaged over the first t0 seconds.
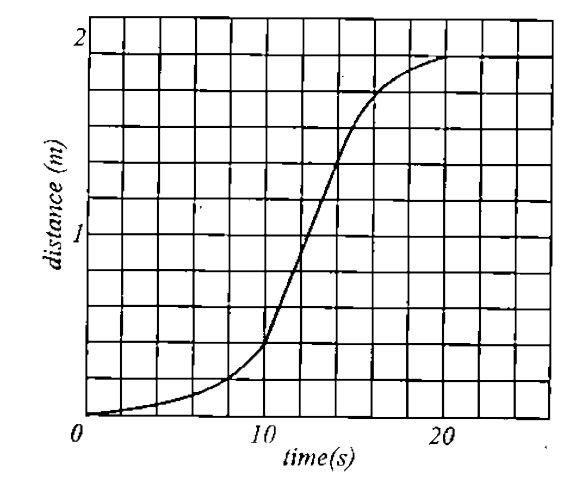
View SolutionA particle moves on the circumference of a circle of radius r. Starting from one point particle reaches to its diametric end in time t.The magnitude of average velocity of the particle is
View SolutionIf magnitude of average speed and average velocity over a time interval are same, then
View SolutionA particle is moving on a circular path of radius R with uniform angular speed ω. The magnitude of average velocityof particle during time t=0 to t=2π3ω:
View Solution
