The velocity of a particle moving in the positive direction of X-axis varies as v=5√x. Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
12.5ms−2
7.5ms−2
5ms−2
2.5ms−2
The correct Answer is:A
To solve the problem, we need to find the acceleration of a particle whose velocity varies with position according to the equation v=5√x.
Step 1: Understanding the relationship between velocity and position
The given equation for velocity is:
v=5√x
We know that acceleration a can be expressed in terms of velocity v and position x using the chain rule:
a=dvdt=dvdx⋅dxdt=dvdx⋅v
This means we need to find dvdx.
Step 2: Differentiate the velocity with respect to position
To find dvdx, we differentiate v=5√x:
dvdx=ddx(5√x)=5⋅12√x=52√x
Step 3: Substitute v into the acceleration formula
Now we can substitute v and dvdx into the acceleration formula:
a=dvdx⋅v=(52√x)⋅(5√x)=25√x2√x=252
Step 4: Conclusion
The acceleration of the particle is:
a=12.5m/s2
Final Answer
The acceleration of the particle is 12.5m/s2.
---
The given equation for velocity is:
v=5√x
We know that acceleration a can be expressed in terms of velocity v and position x using the chain rule:
a=dvdt=dvdx⋅dxdt=dvdx⋅v
This means we need to find dvdx.
To find dvdx, we differentiate v=5√x:
dvdx=ddx(5√x)=5⋅12√x=52√x
Now we can substitute v and dvdx into the acceleration formula:
a=dvdx⋅v=(52√x)⋅(5√x)=25√x2√x=252
The acceleration of the particle is:
a=12.5m/s2
The acceleration of the particle is 12.5m/s2.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.5
25 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.6
20 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.3
10 Videos
- MOTIONBOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
The velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
View SolutionThe velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.
View Solution
Knowledge Check
The velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
AThe initial velocity of the particle is zeroBthe initial velocity of the particle is 2.5ms.CThe accelration of the particle is 2.5ms2.DThe acceleration of the particle is 50ms2.The acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is 0.8ms−1 at x = 0, then velocity of the particle at x=1.4m is (∈ms−1).
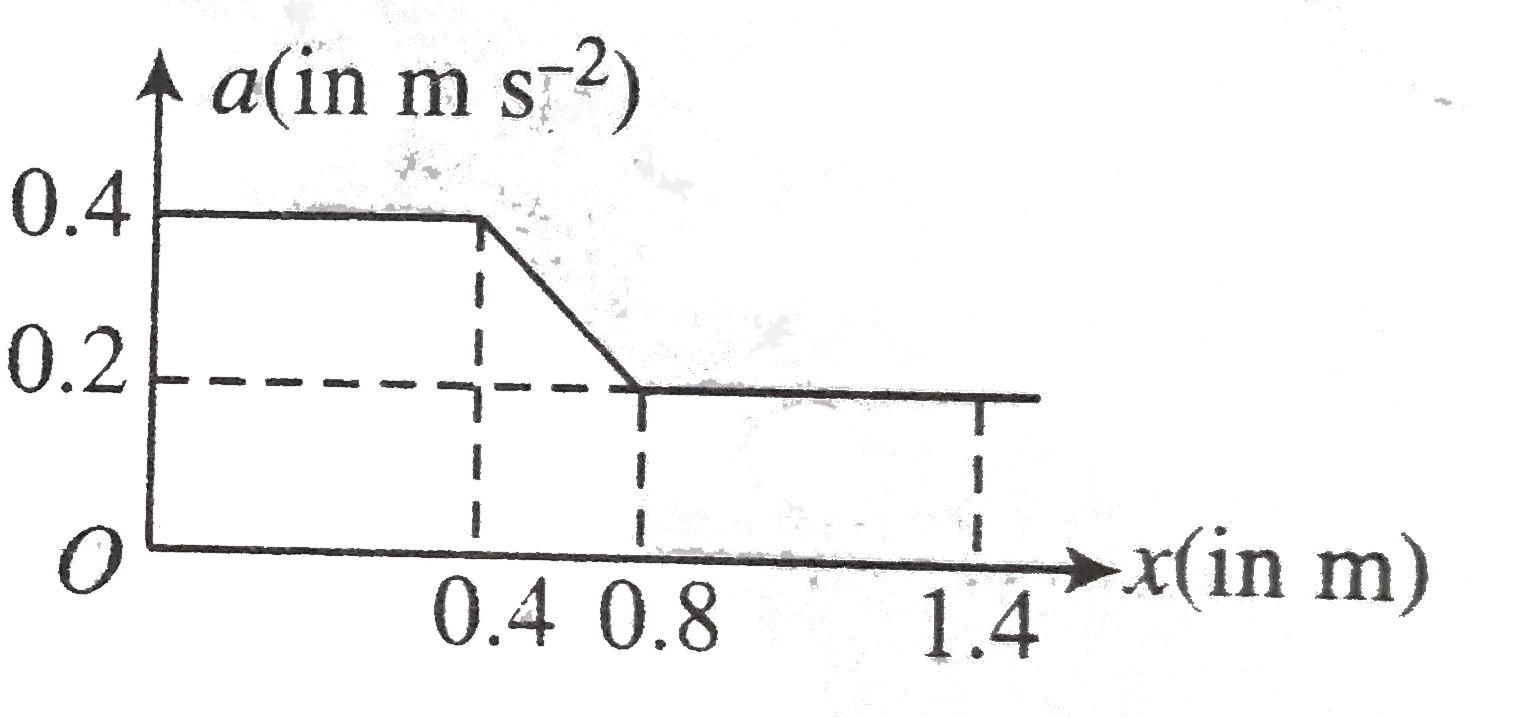 A1.6B1.2C1.4DNone of these
A1.6B1.2C1.4DNone of these
The velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.
View SolutionThe velocity of a particle moving in the positive direction of x-axis varies as v=α√x where α is positive constant. Assuming that at the moment t=0, the particle was located at x=0, find (i) the time dependance of the velocity and the acceleration of the particle and (ii) the mean velocity of the particle averaged over the time that the particle takes to cover first s meters of the path.
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionThe velocity-position graph of a particle moving in a straight line along x-axis is given below. Acceleration of particle at x = 2 m is
View SolutionThe velocity-position graph of a particle moving in a straight line along x -axis is given below.Acceleration of particle at x=2m is
View Solution
