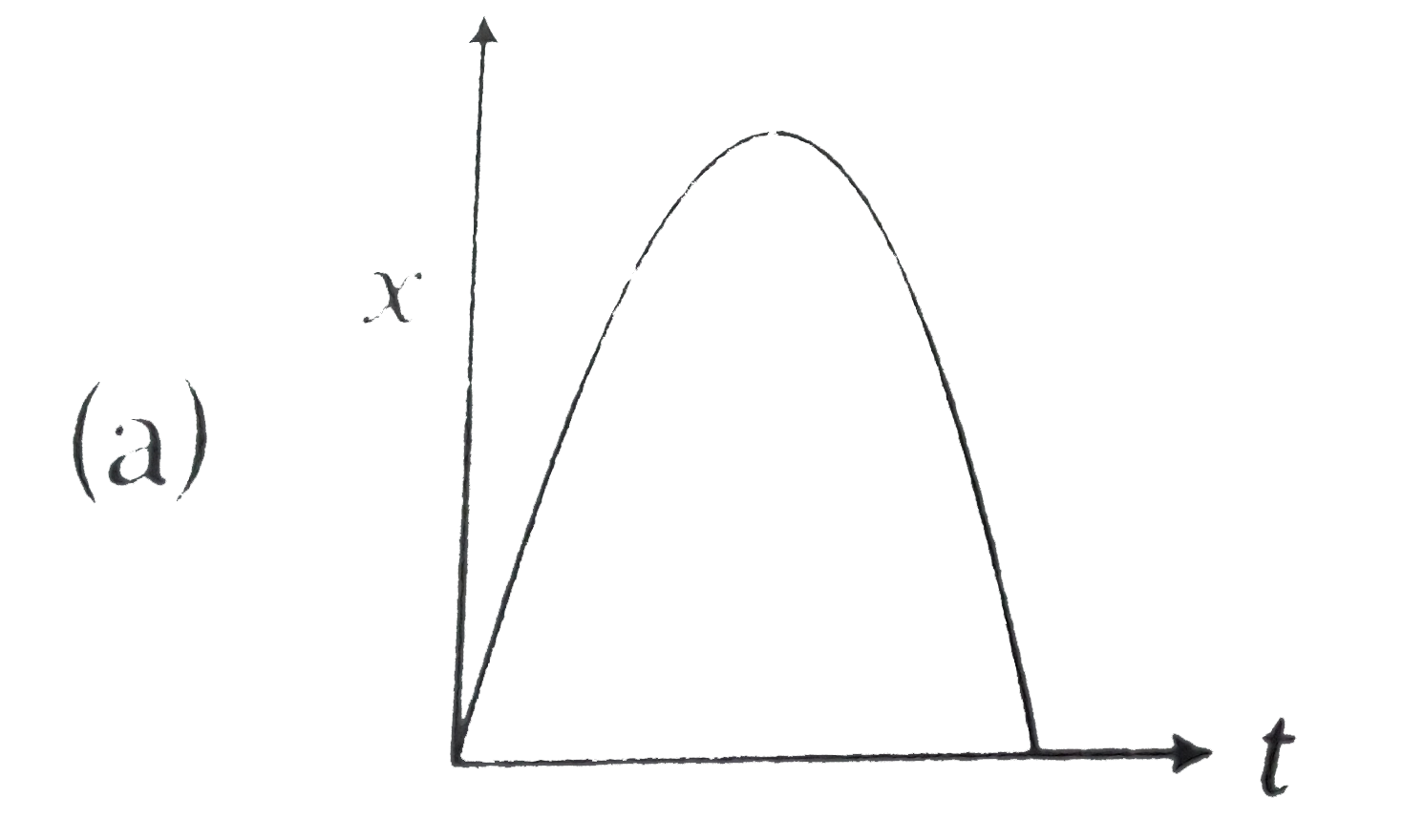
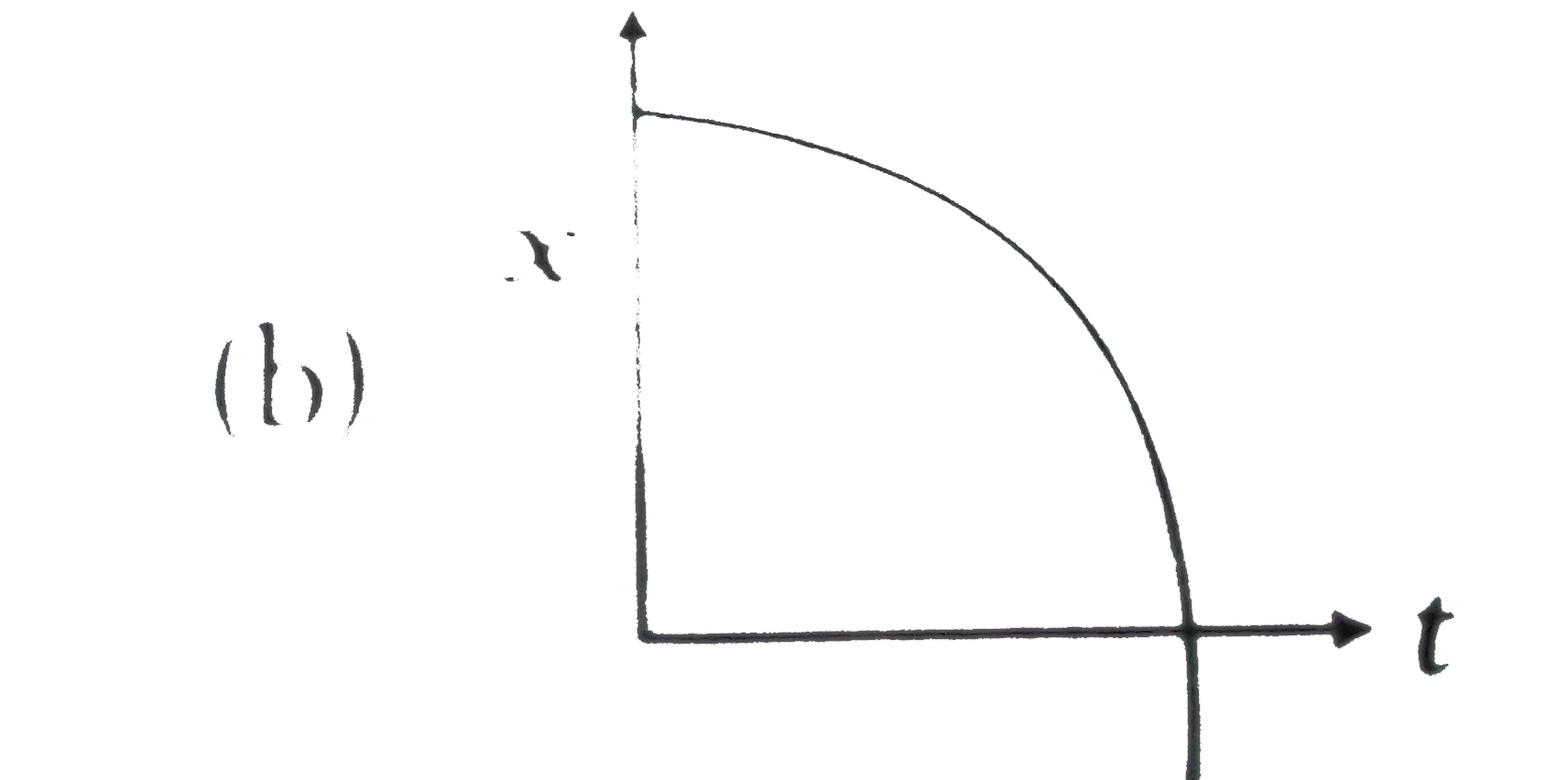
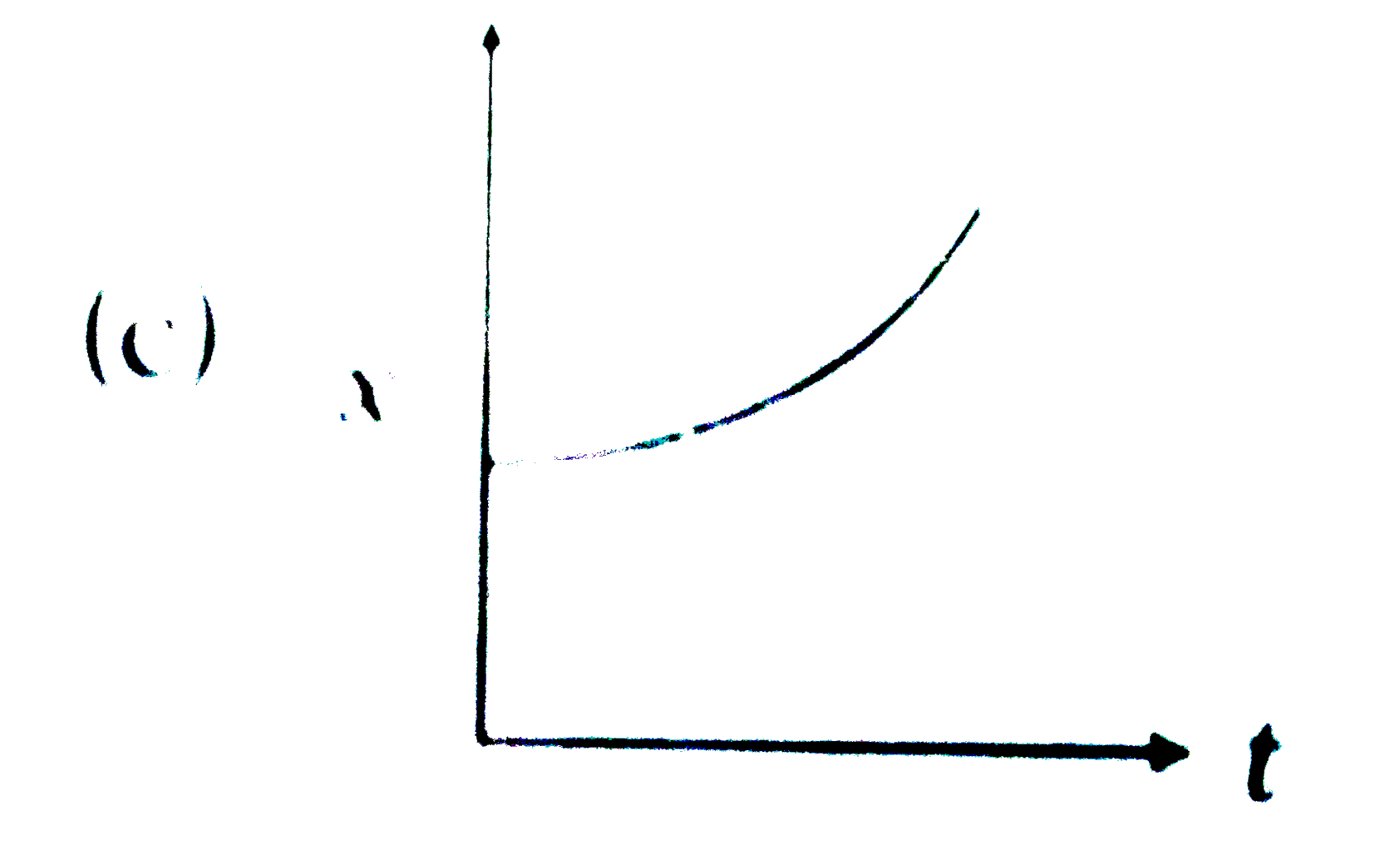
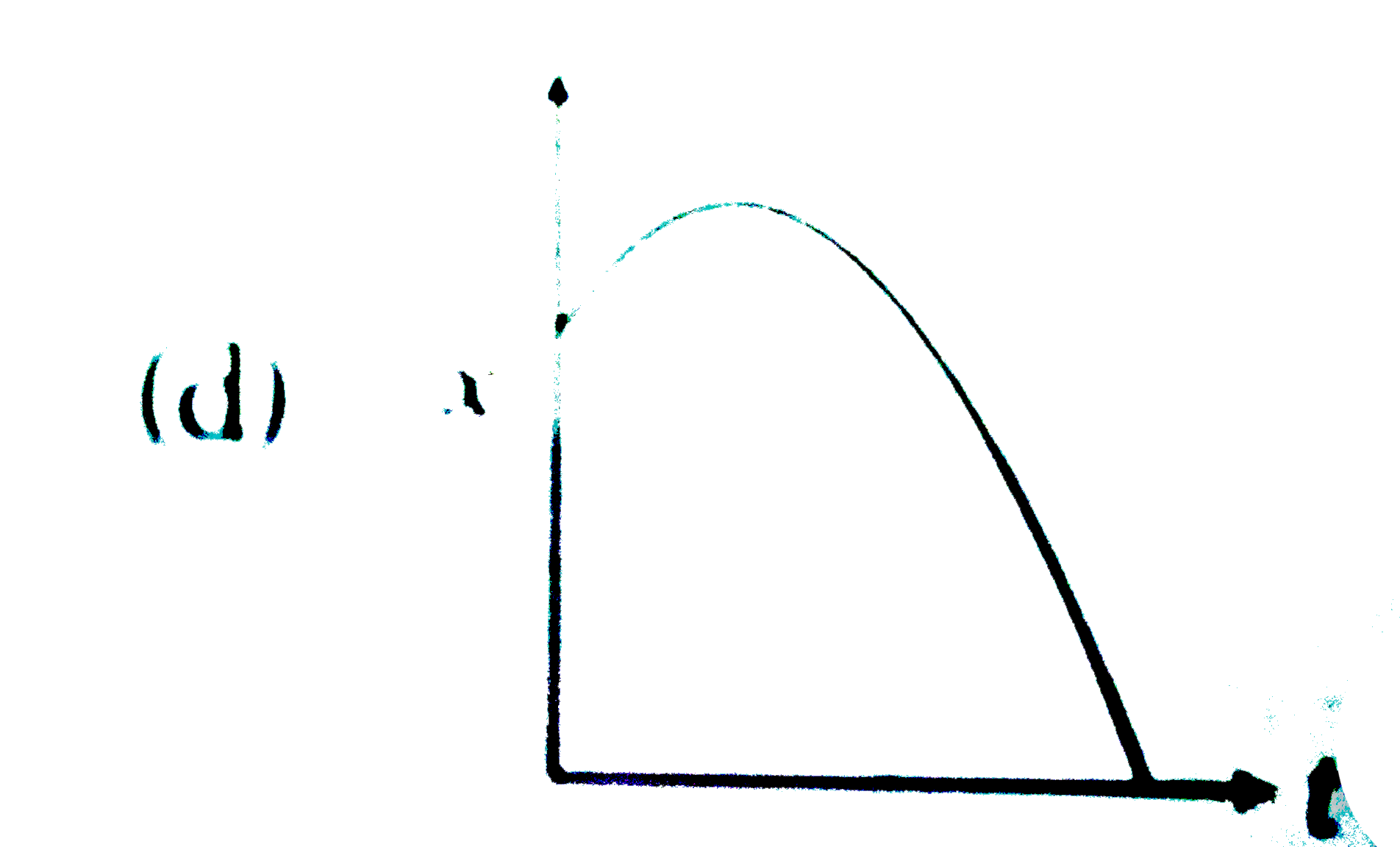
The displacement x of a particle in a straight line motion is given by $x = 1 - t - t^{2}$ . The correct representation of the motion is

A

ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$\frac{d x}{d t} = υ = 1 - 2 t$
Comparing with $υ = u + a t$ , we have, $u = - 1 m s^{- 1}$ and
$a = - 2 m s^{- 2}$
At t = 0, x = 1m. Then, u and a both are negative. Hence, x-coordinate of particle will go on decreasing.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The displacement x of a particle along a straight line at time t is given by $x = a_{0} + a_{1} t + a_{2} t^{2}$ . The acceleration of the particle is
A $a_{0}$
B $a_{1}$
C $2 a_{2}$
D $a_{2}$
Question 2 - Select One
The displacement x of a particle at time t along a straight line is given by $x = α - β t + γ t^{2}$ . The acceleraion of the particle is
A $- β$
B $- β + 2 γ$
C $2 γ$
D $- 2 γ$
Question 3 - Select One
The displacement 'x' of a particle moving along a straight line at time t is given by $x = a_{0} + a_{1} t + a_{2} t^{2}$ . The acceleration of the particle is :-
A $a_{1}$
B $a_{2}$
C $2 a_{2}$
D $3 a_{2}$

DC PANDEY-MOTION IN A PLANE-(A) Taking it together

Home
Ask Doubt
Profile