A point moving with constant acceleration from A to B in the straight line AB has velocities u and v at and B respectively. Find its velocity at C, the mid point of AB. Also show that if the time from A to C is twice that from C to B, then v=7u.
5 u
6 u
7 u
8 u
The correct Answer is:C
According to question, the diagram can be drawn as
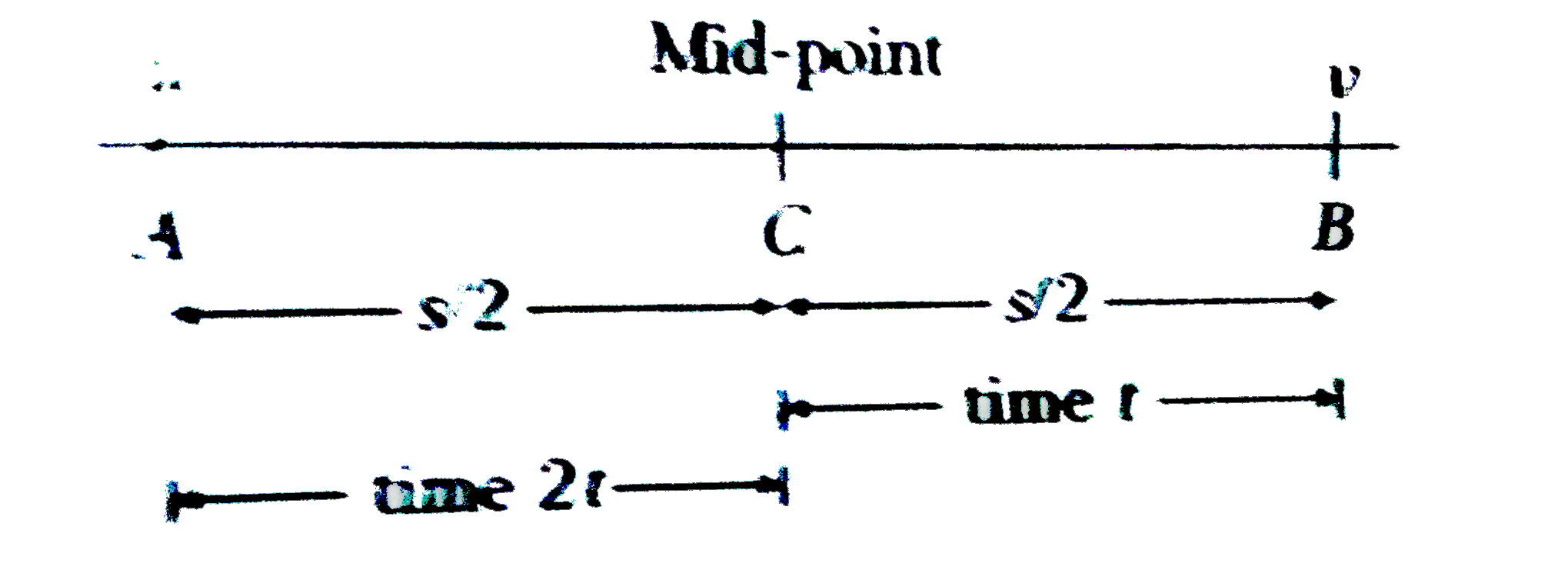
For motion from A to C
s2=ut+12a×(2t)2=2ut+2at2
Also, for motion from C to B. (Let initial velocity be υ')
s2=(u+2at)t+!2at2 (∴υ'=u+2at)
=ut+2at2+12at2
Now, 2ut+2qat2=ut+2at2+12at2⇒u=at2
For overall motion,
υ=u+3at=at2+3at=7at2=7u (∴u=at2)
Topper's Solved these Questions
- MOTION IN A PLANEBook:DC PANDEYChapter:MOTION IN A PLANEExercise:(B) Meical entrance special format questions (Mathch the columns)
Explore 6 Videos
- MOTIONBook:DC PANDEYChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- PROJECTILE MOTIONBook:DC PANDEYChapter:PROJECTILE MOTIONExercise:Level - 2 Subjective
Explore 10 Videos
Similar Questions
(a) A particle moving with constant acceleration from A to B in a straight line AB has velocities u and v at A and B respectively. Find the velocity of the particle at the midpoint of AB.
(b) If the time taken by the particle to go from A to the midpoint of AB is two times that from the midpoint of AB to B then find the value of v/u.
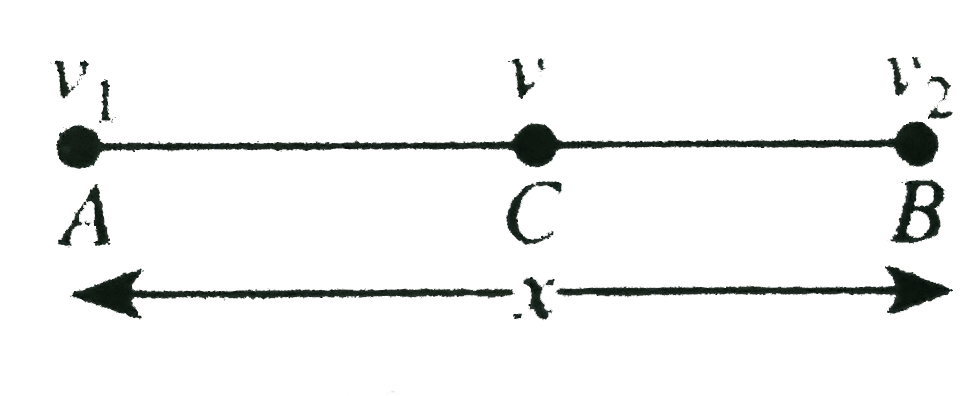
View SolutionA particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
 .
.
View Solution
Knowledge Check
A body is moving with constant acceleration, a=5ms2 from A to B in straight line AB. The velocity of particle at A and B are 5 m/s and 15 m/s respectively. The velocity at mid-point of AB is
A√125msB√250msC√550msD√600msA particle is moving with uniform acceleration along a straight line ABC. Its velocity at A and B are 6 m/s and 9 m/s respectively if AB:BC=5:16 then its velocity at C is
A9.6m/s2B12m/sC15m/sD21.5m/sFor body moving with uniform acceleration a, initial and final velocities in a time interval t are u and v respectively. Then its average velocity in the time interval t is
A(v+at)B(v−at2)C(v−at)D(u−at2)
A particle moves along a straight line AB with constant acceleration. Its velocities are u and v at A and B, respectively. Show that its velocity at the mid-point of AB is √u2+v22.
View SolutionA particle is moving with uniform acceleration along a straight line "ABC" .Its velocity at A and B are 6m/s" and "9m/s respectively. If AB:BC=5:16" then its velocity at C is
View SolutionTwo ends of a train moving with a constant acceleration pass a certain point with velcities uandv. Show that the velocity with which the middle point of the train passes the same point is sqrt(9u"^(2) +v^(2)//2).
View Solutiona particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionA particle starting from a point A and moving with a positive constant acceleration along a straight line reaches another point B in time T. Suppose that the initial velocity of the paticle is u > 0 and P is the midpoint of the line AB. If the velocity of the particle at point P is ν1, and if the velocity at time T/2 is ν2, then
View Solution