A block is placed at the top of a smooth hemisphere of radius $R$ . Now the hemisphere is given a horizontal acceleration $a_{0}$ . Find the velocity of the block relative to the hemisphere as a function of $θ$ at it slides down.

Video Solution

Text Solution

Verified by Experts

In the reference frame of hemisphere. Apply a pseudo force on m.

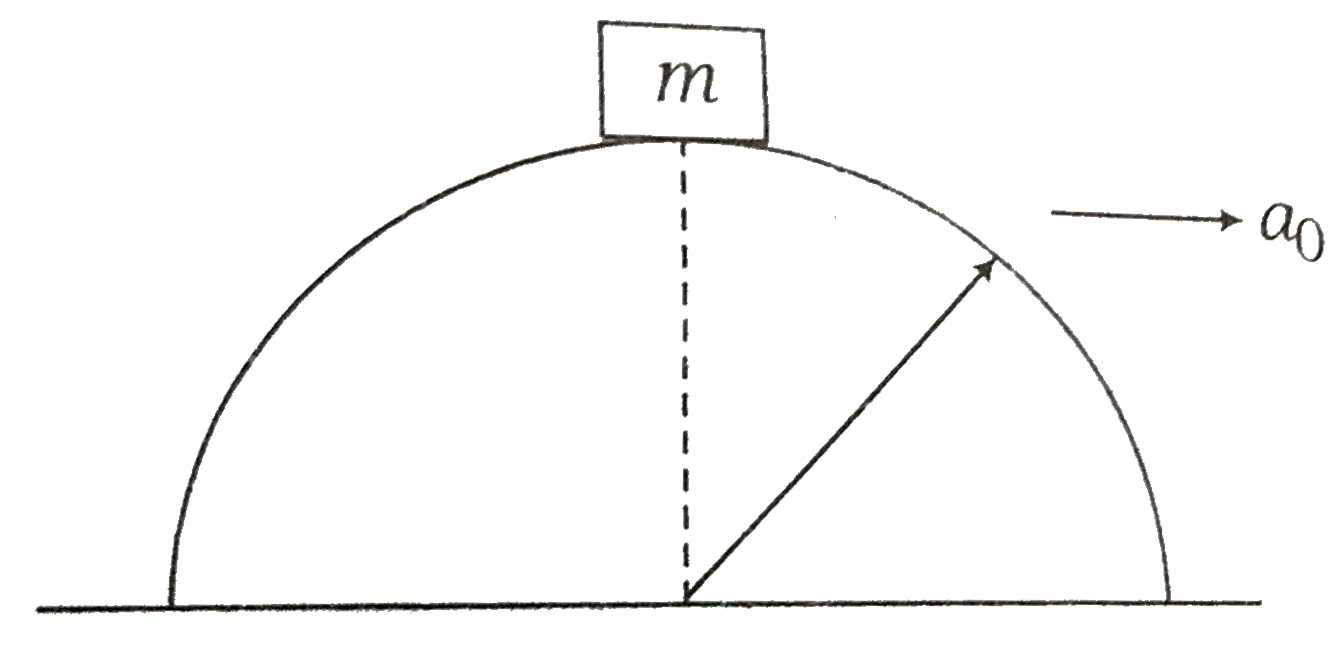
From the work-energy theorem,

$W_{total} = Δ K \Rightarrow W_{g r} + W_{p s e u d o} = Δ K$
$m g R (1 - cos θ) + m a_{0} R sin θ = \frac{1}{2} m v^{2} - 0$
$v = \sqrt{2 R {g (1 - cos θ) + a_{0} sin θ)}}$
The work done by normal reaction N is zero because it is always perpendicular to displacement.

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A small ball is placed at the top of a smooth hemispherical wedge of radius $R$ . If the wedge is accelerated with an acceleration $a$ , find the velocity of the ball relative to wedge as a function of $θ$ .

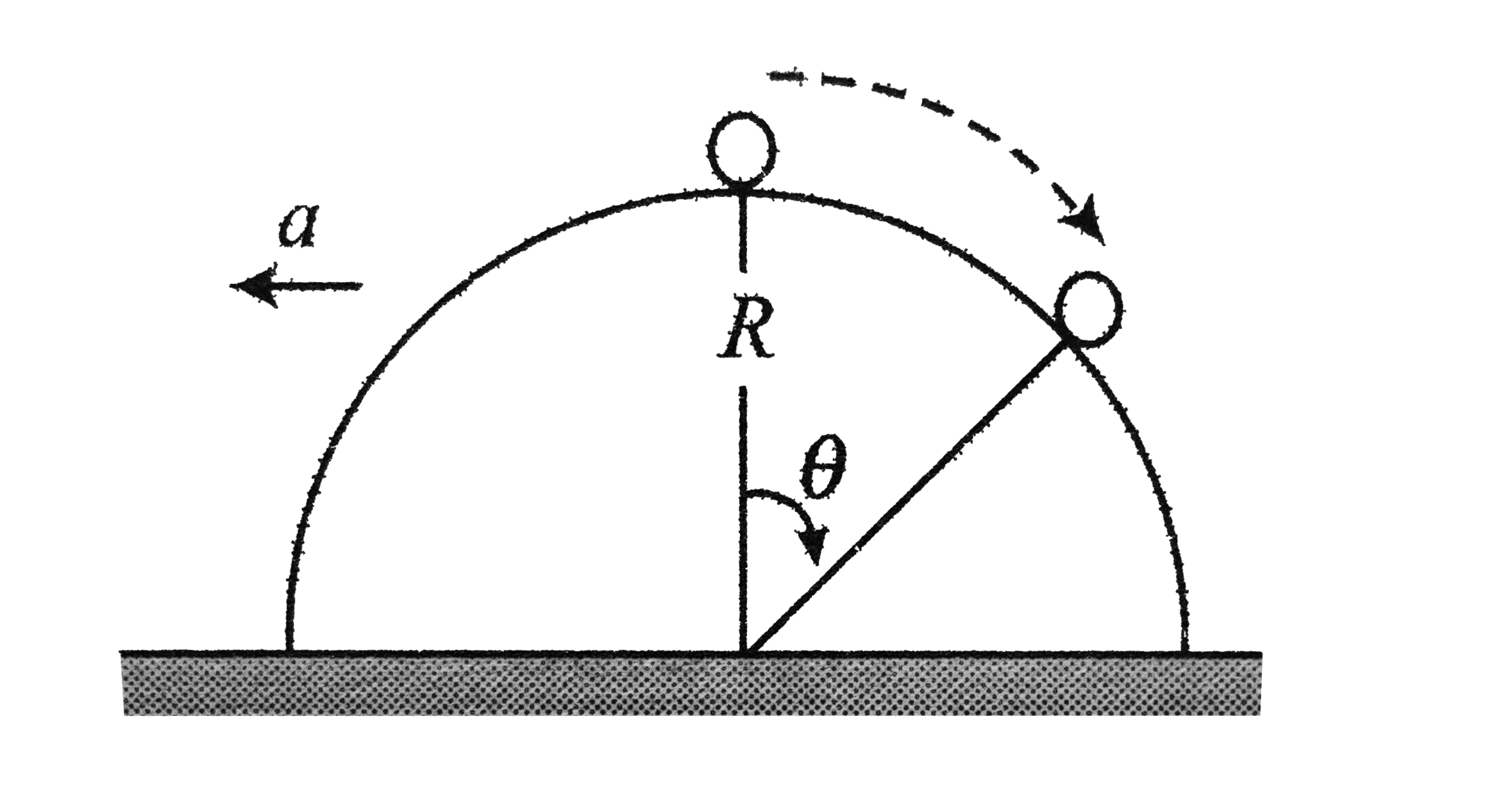A $\sqrt{2 R [g (1 - sin θ) + a R cos θ]}$
B $\sqrt{2 R [g (1 + cos θ) - a R sin θ]}$
C $\sqrt{2 R [g (1 - cos θ) + a R sin θ]}$
D $\sqrt{2 R [g (1 + sin θ) - a R cos θ]}$
Question 2 - Select One
A small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration $a_{0} = g$ . The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is

A $\sqrt{\frac{g R}{3}}$
B $\sqrt{\frac{2 g R}{3}}$
C $\sqrt{\frac{5 g R}{3}}$
D $\sqrt{\frac{7 g R}{3}}$
Question 3 - Select One
A body rest on the top of a hemisphere of radius R. What will be the least horizontal velocity imparted to it , if it has to leave the hemisphere without sliding down?
A $\sqrt{2 g R}$
B $\sqrt{5 g R}$
C $\sqrt{g R}$
D $\sqrt{3 g R}$

DC PANDEY-WORK, ENERGY AND POWER-MEDICAL ENTRACES GALLERY

Home
Ask Doubt
Profile