Question

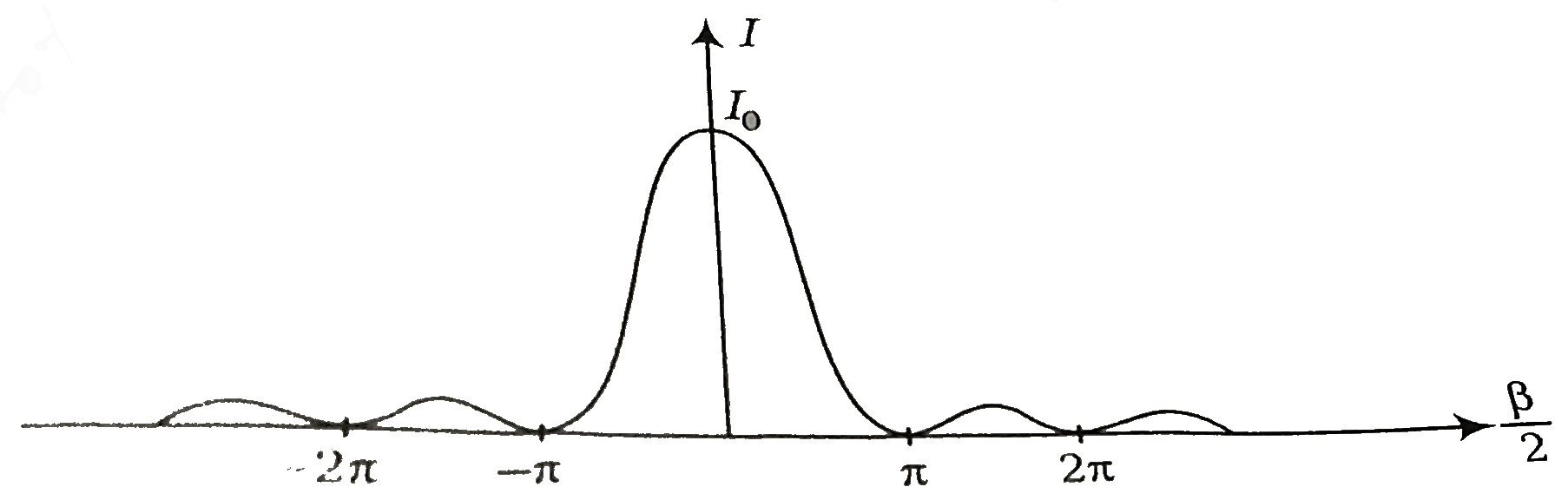
In Young’s double-slit experiment, the distance between the two identical slits is ${\displaystyle 6.1}$ times larger than the slit width. Then the number of intensity maxima observed within the central maximum of the single-slit diffraction pattern is

Options

A. 3
B. 6
C. 24
D. 12

Answer

D

Explanation

To solve the problem, we need to determine the number of intensity maxima observed within the central maximum of the single-slit diffraction pattern in Young's double-slit experiment.

1. Define the Variables:
- Let \( a \) be the width of each slit.
- Let \( d \) be the distance between the two slits.
- According to the problem, \( d = 6.1a \).

2. Width of the Central Maximum:
- The width of the central maximum of a single-slit diffraction pattern is given by the formula:
\( \text{Width of central maximum} = \frac{2\lambda D}{a} \)
where \( \lambda \) is the wavelength of light and \( D \) is the distance from the slits to the screen.

3. Width of the Central Maximum in Double-Slit Experiment:
- The width of the central maximum in the double-slit experiment can also be expressed in terms of the distance between the slits:
\( \text{Width of central maximum} = \frac{2\lambda D}{d} = \frac{2\lambda D}{6.1a} \)

4. Setting the Widths Equal:
- To find the number of maxima (\( n \)) within the central maximum of the single-slit diffraction pattern, we equate the widths:
\( n \cdot \frac{2\lambda D}{6.1a} = \frac{2\lambda D}{a} \)

5. Simplifying the Equation:
- We can cancel \( 2\lambda D \) from both sides:
\( n \cdot \frac{1}{6.1} = 1 \)
- Thus, we find:
\( n = 6.1 \)

6. Rounding Down:
- Since \( n \) must be an integer (as it represents the number of maxima), we round down \( 6.1 \) to get:
\( n = 6 \)

Conclusion:
The number of intensity maxima observed within the central maximum of the single-slit diffraction pattern is 6.