An electron falls from rest through a vertical distance h in a uniform and vertically upward directed electric field E. the direction of electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h.The time of fall of the electron, in comparison to the time of flal of the proton is
10 times greater
5 times greater
smaller
equal
The correct Answer is:C
Force on a charged particle in the presence of an electric field is given as
F=qE………(i)
Where, q is the charge on the charged particle and E is the electric field.
From Newton's second law of motion, force on a particle with mass m is given as
F=ma..............(ii)
From Eqs. (i) and (ii), we get
F=ma=qE⇒a=qEm..........(iii)
Now, consider that a particle falls from rest through a vertical distance h. Therefore, u=0 andthe second equation of motion becomes
s=ut+12at2
or h=0×t+12at2
=12×qEmt2 from Eq. (iii)
⇒t2=2hmqE or t=√2hmqE
since, the particle given in the question is electron and proton, and the quantitiy √2hqE (here, qp=qe=e) for both of them is constant. Thus, we can write
t=k√m
Where, k=√2hqE or t∝√m
As, mass of proton mp>> mass of electron (me. Thus,the time of fall of an electron would be smaller than the time of fall of a protons.
Topper's Solved these Questions
- SOLVED PAPERS 2018BOOK - DC PANDEYCHAPTER - SOLVED PAPERS 2018EXERCISE - AIIMS
22 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEYCHAPTER - SOLVED PAPERS 2018EXERCISE - Assertion and Reasons
10 Videos
- SOLVED PAPER 2017BOOK - DC PANDEYCHAPTER - SOLVED PAPER 2017EXERCISE - Solved papers 2017(JIPMER)
32 Videos
- WAVE OPTICSBOOK - DC PANDEYCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced E. Integer Type Questions
13 Videos
Similar Questions
An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View Solution
Knowledge Check
An electron falls from rest through a vertical distance h in a uniform and vertically upwards directed electric field E. The direction of electric field is now reversed , keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall proton is
A10 times greaterB5 times greaterCSmallerDEqualAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
ASame in both casesBMore in the case of electronCMore in the case of protonDIndependent of charge
An electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
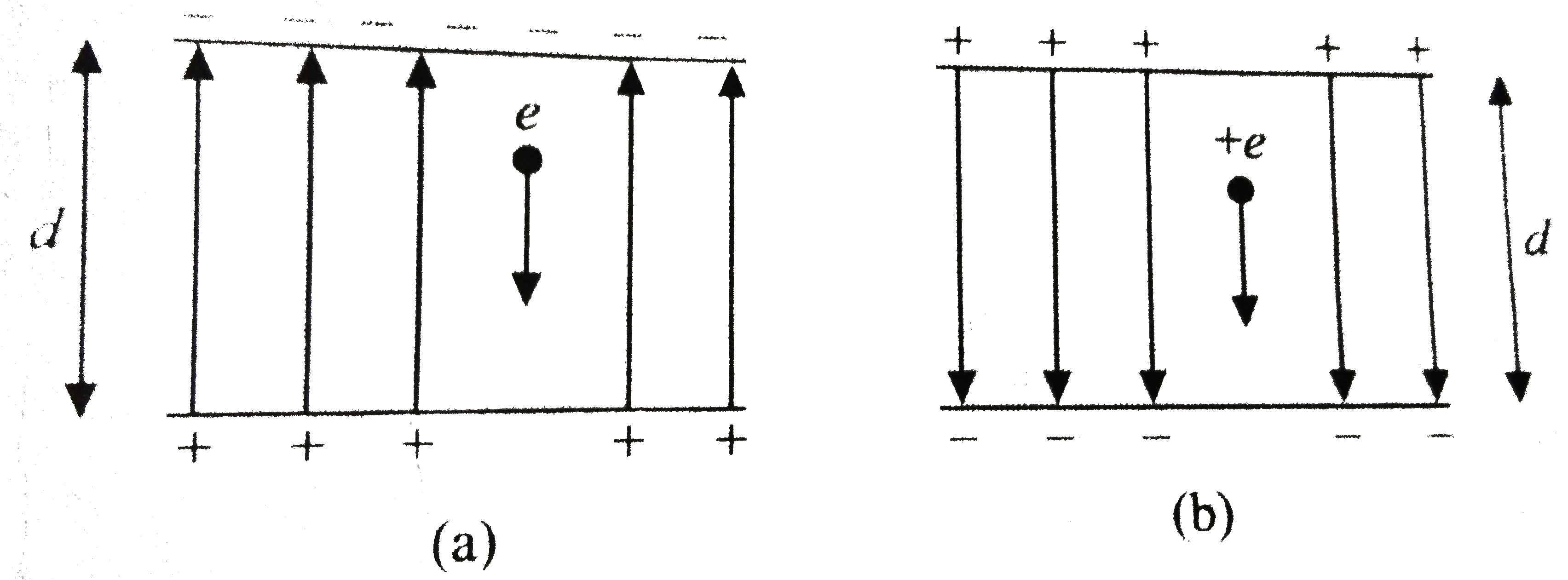 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View SolutionAn electron and a proton travel through equal distances in the same uniform electric field E. Compare their time of travel. (Neglect gravity)
View SolutionAn electron falls through a distance of 1.5cm in a uniform electric field of value 2×104N/C, opposite to direction of fall. Compare the time of fall with 'free fall under gravity'.
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
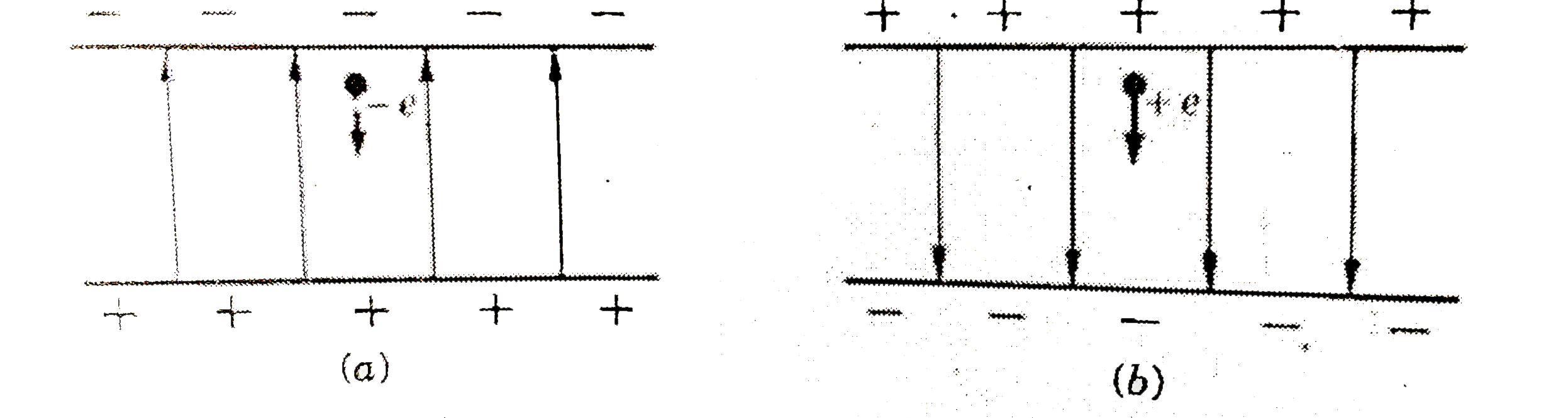
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.

View Solution
