An electron and a proton travel through equal distances in the same uniform electric field E. Compare their time of travel. (Neglect gravity)
To compare the time of travel of an electron and a proton through equal distances in the same uniform electric field, we can follow these steps:
Step 1: Understand the Forces Acting on the Particles
In a uniform electric field E, a force F acts on a charged particle given by the equation:
F=qE
where q is the charge of the particle.
Step 2: Calculate the Forces on the Electron and Proton
- For the electron (charge −e):
Fe=−eE
The direction of the force is opposite to the electric field.
- For the proton (charge +e):
Fp=eE
The direction of the force is in the same direction as the electric field.
Step 3: Apply Newton's Second Law
Using Newton's second law F=ma, we can express the acceleration of each particle:
- For the electron:
Fe=meae⟹−eE=meae⟹ae=−eEme
- For the proton:
Fp=mpap⟹eE=mpap⟹ap=eEmp
Step 4: Use the Kinematic Equation
Assuming both particles start from rest and travel the same distance d, we can use the kinematic equation:
d=ut+12at2
Since both start from rest, u=0, so the equation simplifies to:
d=12at2
Step 5: Solve for Time of Travel
- For the electron:
d=12aet21⟹d=12(−eEme)t21
This gives:
t21=2dmeeE
- For the proton:
d=12apt22⟹d=12(eEmp)t22
This gives:
t22=2dmpeE
Step 6: Compare the Times
Now we can compare t1 and t2:
t21t22=memp
Taking the square root gives:
t1t2=√memp
Conclusion
Since the mass of the electron me is much smaller than the mass of the proton mp, we conclude that:
t1<t2
Thus, the electron takes less time to travel the same distance compared to the proton.
In a uniform electric field E, a force F acts on a charged particle given by the equation:
F=qE
where q is the charge of the particle.
- For the electron (charge −e):
Fe=−eE
The direction of the force is opposite to the electric field.
Fp=eE
The direction of the force is in the same direction as the electric field.
Using Newton's second law F=ma, we can express the acceleration of each particle:
- For the electron:
Fe=meae⟹−eE=meae⟹ae=−eEme
Fp=mpap⟹eE=mpap⟹ap=eEmp
Assuming both particles start from rest and travel the same distance d, we can use the kinematic equation:
d=ut+12at2
Since both start from rest, u=0, so the equation simplifies to:
d=12at2
- For the electron:
d=12aet21⟹d=12(−eEme)t21
This gives:
t21=2dmeeE
d=12apt22⟹d=12(eEmp)t22
This gives:
t22=2dmpeE
Now we can compare t1 and t2:
t21t22=memp
Taking the square root gives:
t1t2=√memp
Since the mass of the electron me is much smaller than the mass of the proton mp, we conclude that:
t1<t2
Thus, the electron takes less time to travel the same distance compared to the proton.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (3 MARKS )23videos
ELECTROSTATICS AND CURRENT ELECTRICITY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS6videos
ELECTROSTATICS AND CURRENT ELECTRICITY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - NUMERICALS49videos
ELECTROSTATICS AND CURRENT ELECTRICITY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS7videos
ELECTRONIC DEVICES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C19videos
SAMPLE QUESTION PAPER 2019
Similar Questions
An electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
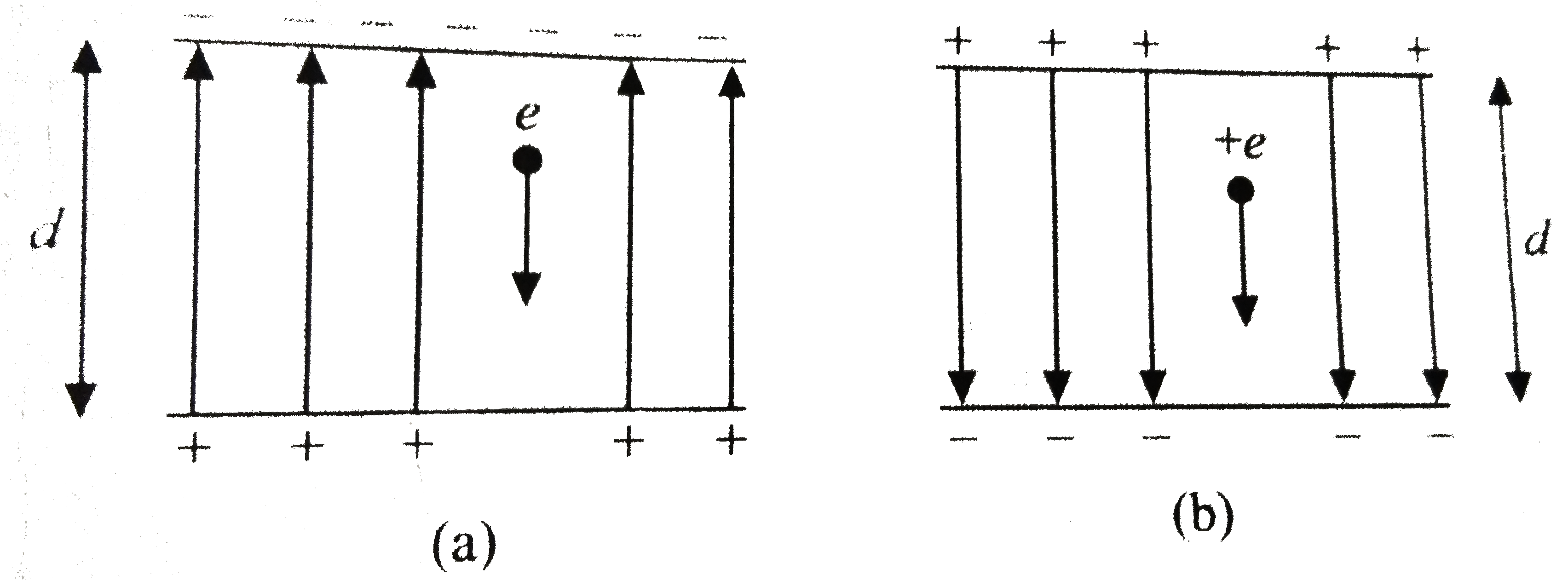 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.View SolutionA proton and an electron are placed in a uniform electric field.
View Solution
Knowledge Check
- Question 1 - Select One
An electron and a proton each travel with equal speeds around circular orbits in the same uniform magnetic field as indicated (not to scale) in Fig. The field is into the page on the diagram. The electron travels ____ arount the _____circle.
 Aclockwise, smaller,couterclockwise, largerBcouterclockwise, larger,clockwise,smallerCclockwise,larger,couterclockwise,smallerDcouterclockwise,larger,clockwise,smaller
Aclockwise, smaller,couterclockwise, largerBcouterclockwise, larger,clockwise,smallerCclockwise,larger,couterclockwise,smallerDcouterclockwise,larger,clockwise,smaller - Question 2 - Select One
An electron and a proton are in uniform electic field. The ratio of their acceleration will be
AZeroBUnityCRatio of masses of proton and electronDRatio of masses of electron and proton - Question 3 - Select One
An electron of mass Me, initially at rest, moves through a certain distance in a uniform electric field in time t1. A proton of mass Mp also initially at rest, takes time t2 to move through an equal distance in this uniform electric field. Neglecting the effect of gravity, the ratio t2/t1 is nearly equal to
A1B√MpMeC√MeMpD1836
An electorn is separated from the proton through a distance of 0.53 Å. Calculate the electric field at the location of the electron.
View SolutionAn electron and proton are placed inside a uniform electric field.
View SolutionAn electron of mass me initially at rest moves through a certain distance in a uniform electric field in time t1. A proton of mass mp also initially at rest takes time t2 to move through an equal distance in this uniform electric field.Neglecting the effect of gravity, the ratio of t2/t1 is nearly equal to
View SolutionAn electron and a proton with equal momentum enter perpendicularly into a uniform magnetic field, then
View SolutionAn electron falls from rest through a vertical distance h in a uniform and vertically upward directed electric field E. the direction of electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h.The time of fall of the electron, in comparison to the time of flal of the proton is
View Solution

