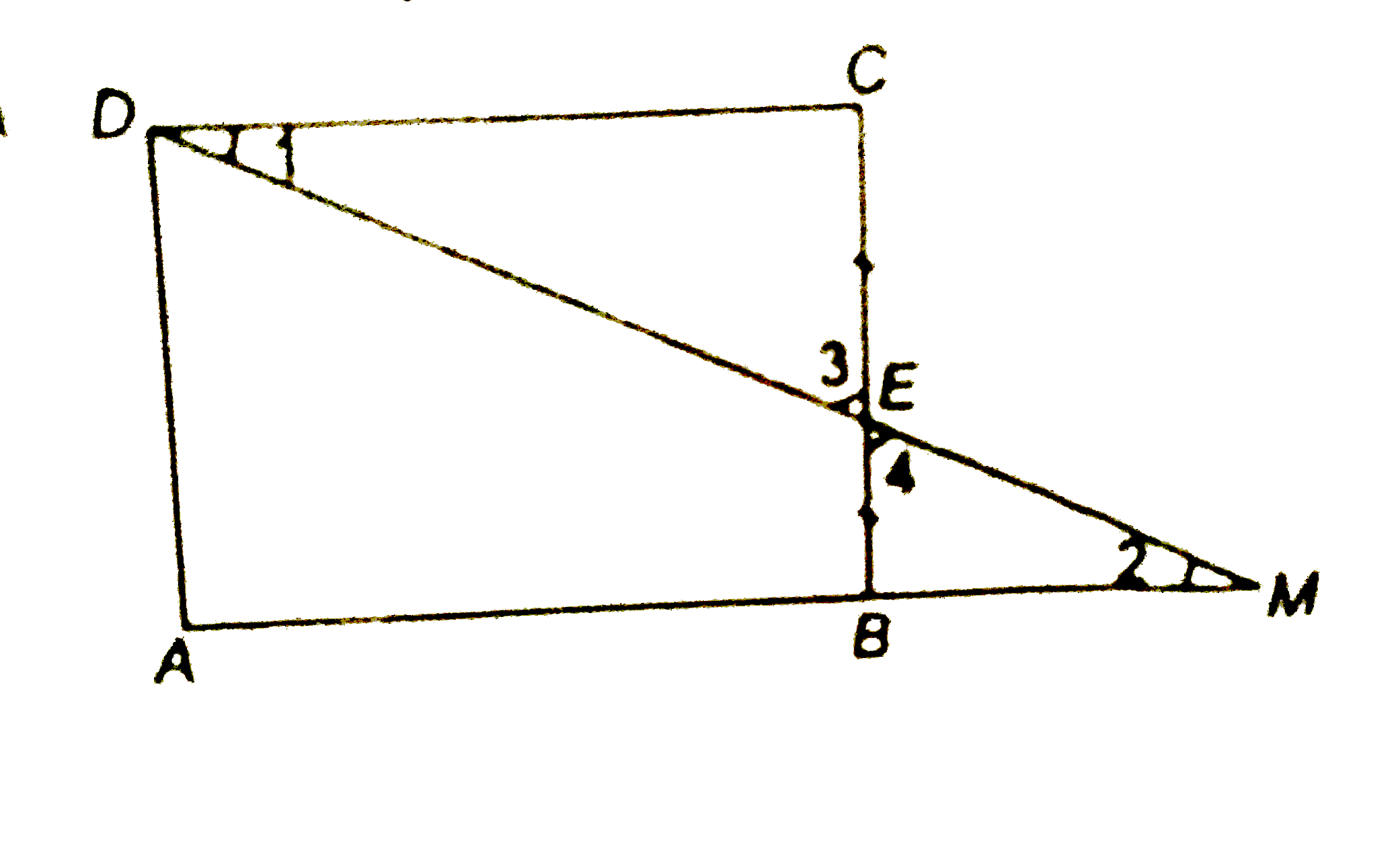
In the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
Video Solution
Text Solution
(i) Since ABCD is a parallelogram
∴ABM||DC
∴∠1=∠2 (alternate angles)
Now, in ΔDCE and ΔMBE
∴⎧⎪⎨⎪⎩∠1=∠2(proved above)∠3=∠4(vertically opposite angles)CE=BE(given as E is the mid-point)
∴ΔDCE≅ΔMBE (AAS) Hence Proved.
(ii) Therefore, DC=MB (c.p.c.t.)
But DC=AB (opposite sides of a parallelogram are equal)
∴AB=MB Hence Proved.
(iii) Now, AM=AB+BM
=DC+DC (poved above)
=2DC Hence Proved.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a35videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2 - Question 2 - Select One
In the adjoining figure a parallelogram ABCD is shown .
AB=24 cm and AO=BO=13 cm. Find BC :
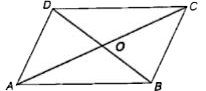 A8 cmB10 cmC11 cmDnone of these
A8 cmB10 cmC11 cmDnone of these - Question 3 - Select One
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AA)AN=√3ABBB)AN=2ABCC)AN2=32AB2DD)AN2=2AB2
In the adjoining figure, ABCD is a parallelogram. If ∠MBC=∠NDA, prove that AM=NC.
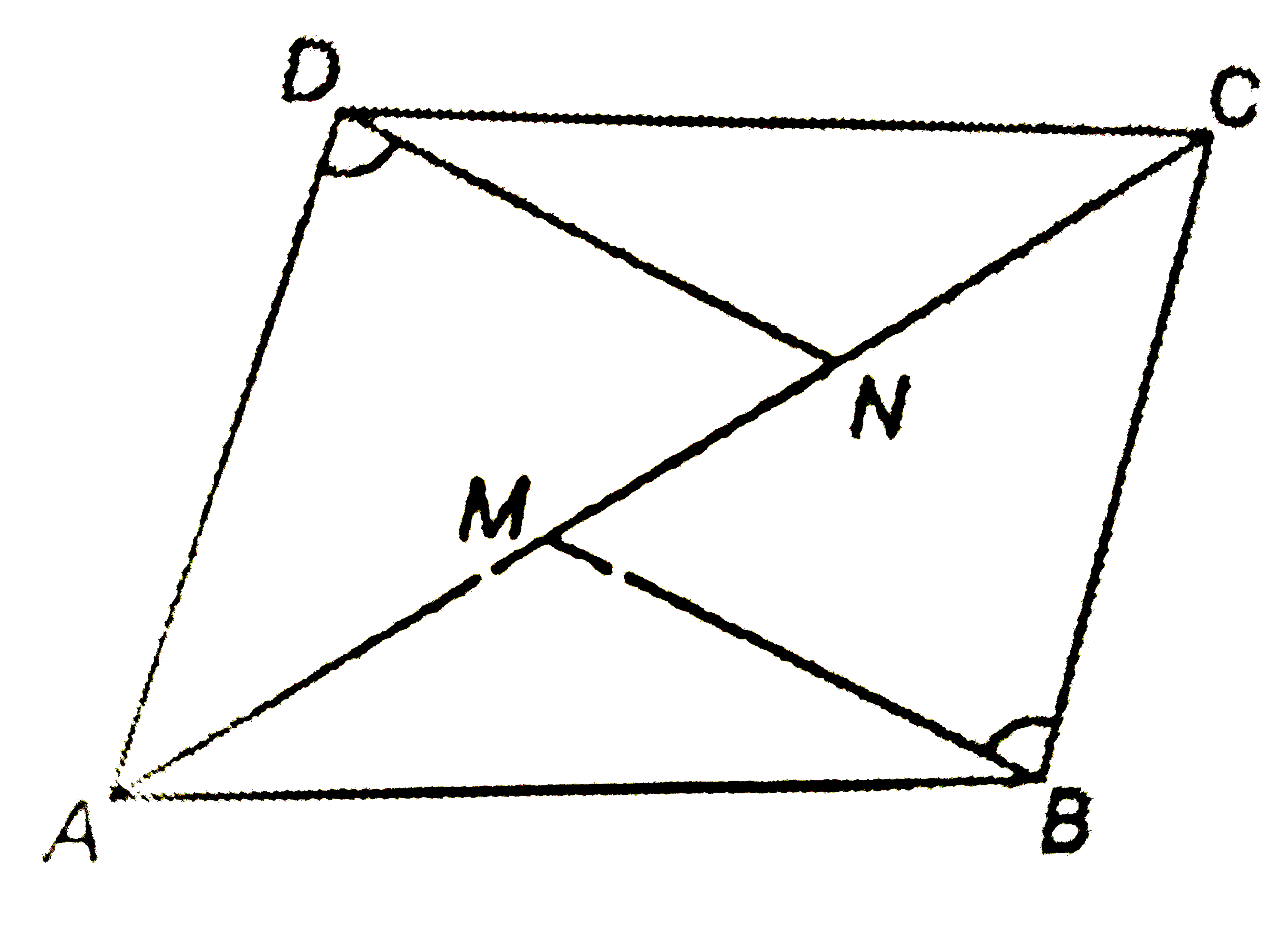 View Solution
View SolutionIn the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
 View Solution
View SolutionIn the given figure ABCD is a parallelogram in which AB||CD and E and F are the mid points of AB and BC respectively. What is the area of ∠BEF?
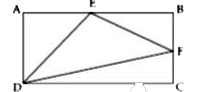 View Solution
View SolutionIn the give figure AB = BC, M is the mid point of AB and N is the mid point of BC, Show that AM = NC
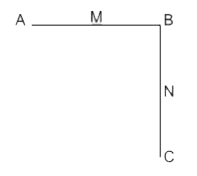 View Solution
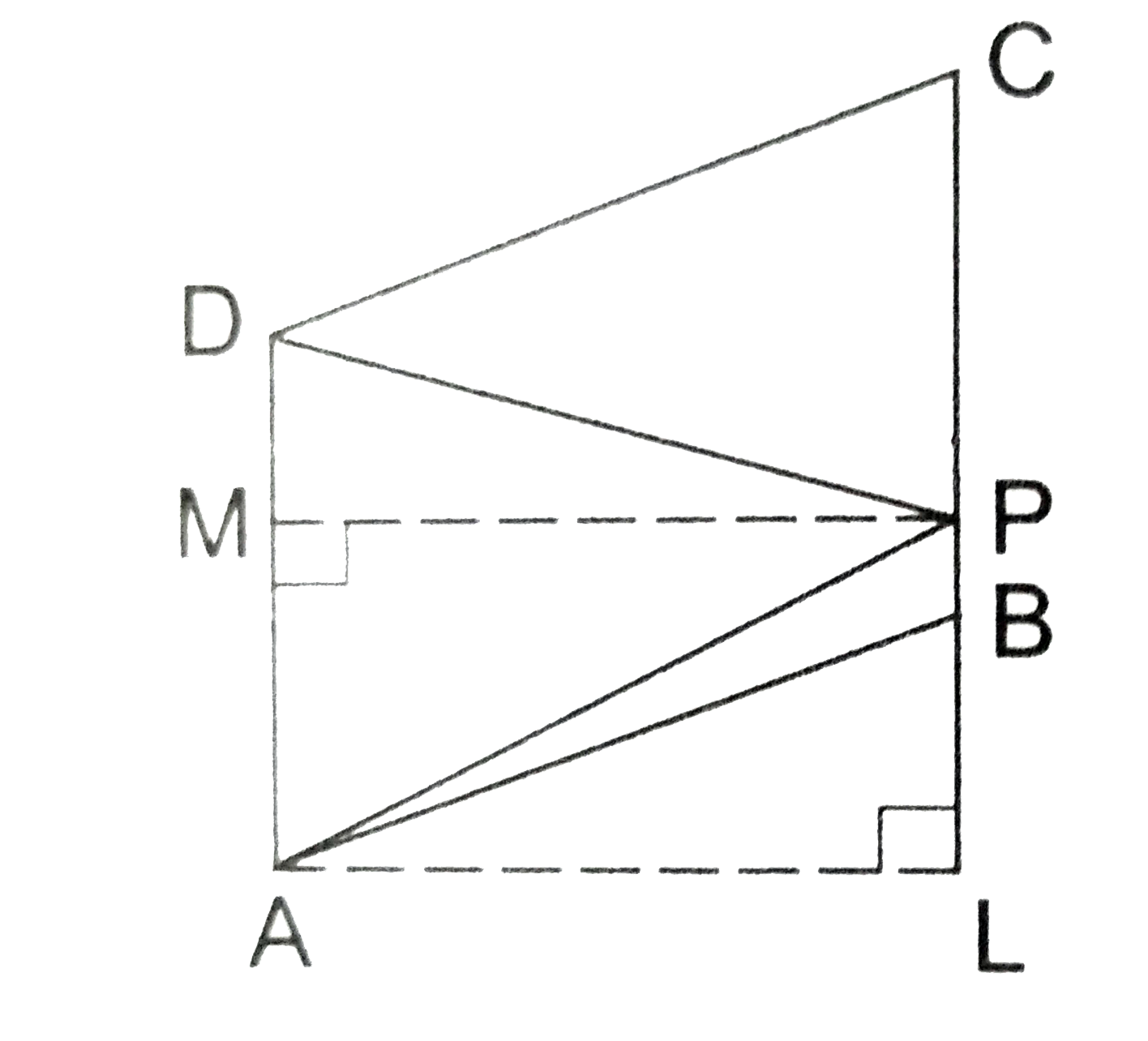
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View Solution


