In the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
Draw AL⊥BCandPM⊥AD.
Since BC||AD, so distance between them remain the same.
∴AL=PM.
=12×BP×AL+12×PC×AL=12×AL×(BP+PC)
=12×AL×BC=12×PM×AD [∴AL=PMandBC=AD]
=ar(△PDA).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
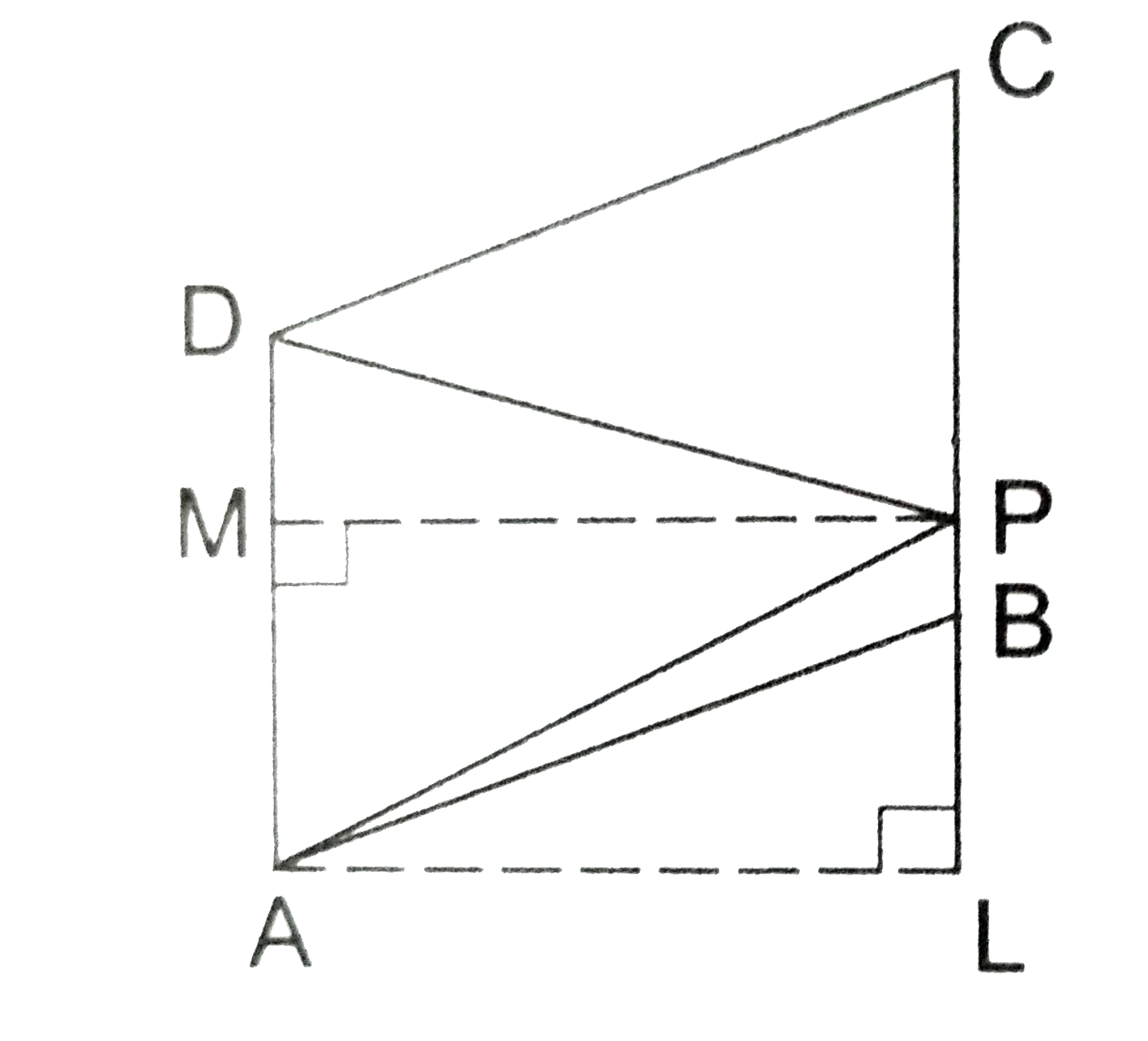
In the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that
ar(△APQ)=ar(△DPQ)=16ar(△ABCD).
View SolutionIn the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar(△ADF)=ar(△DCE).
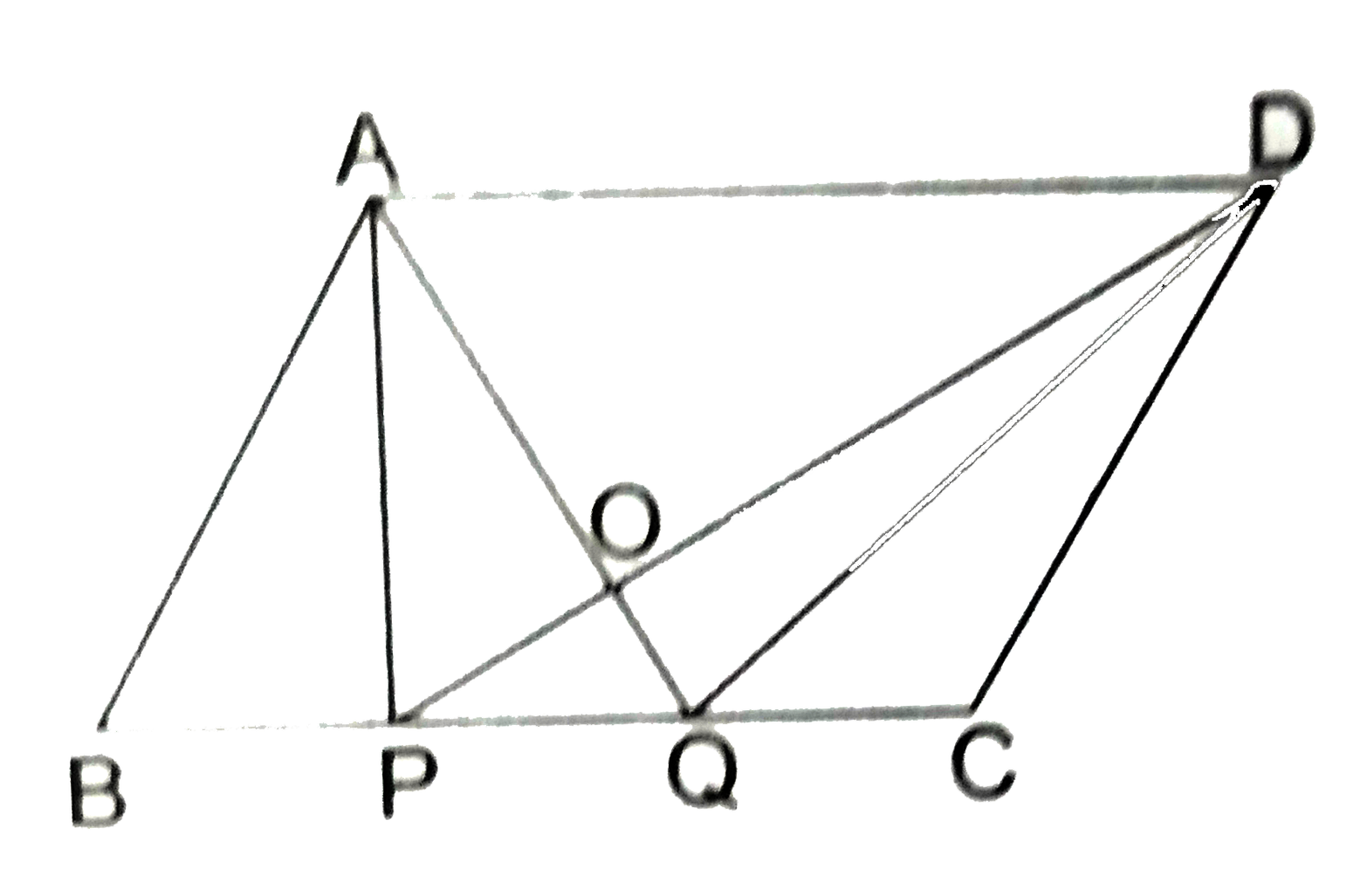
View SolutionIn the adjoining figure, MNPQ and ABPQ are parallelogram and T is any point on the side BP. Prove that
(i) ar(MNPQ)=ar(ABPQ)
(ii)ar(△ATQ)=12ar(MNPQ).
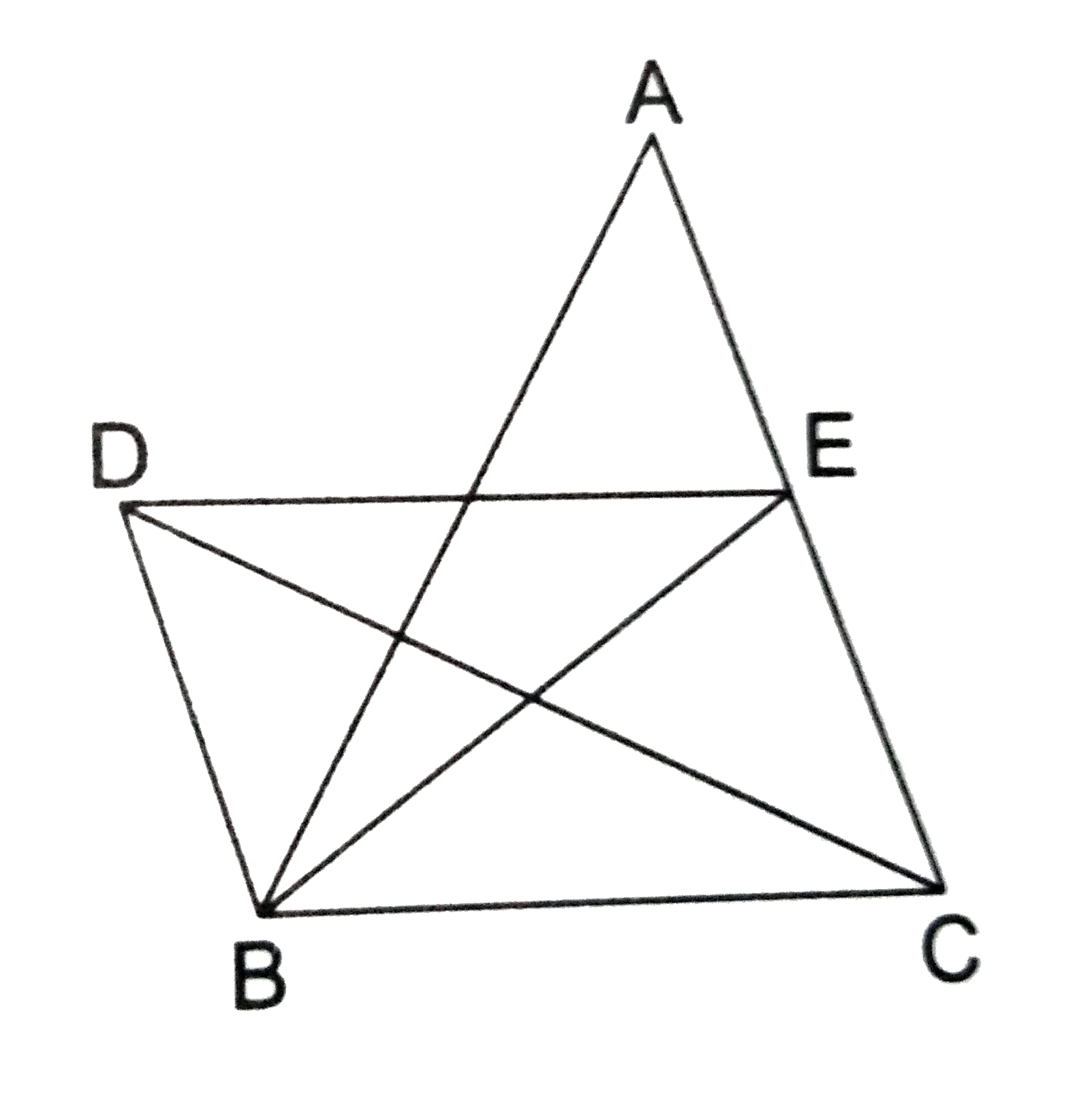
View SolutionIn the adjoining figure, BD||CA, E is the midpoint of CA and BD=12CA. Prove that
ar(△ABC)=2ar(△DBC).
View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
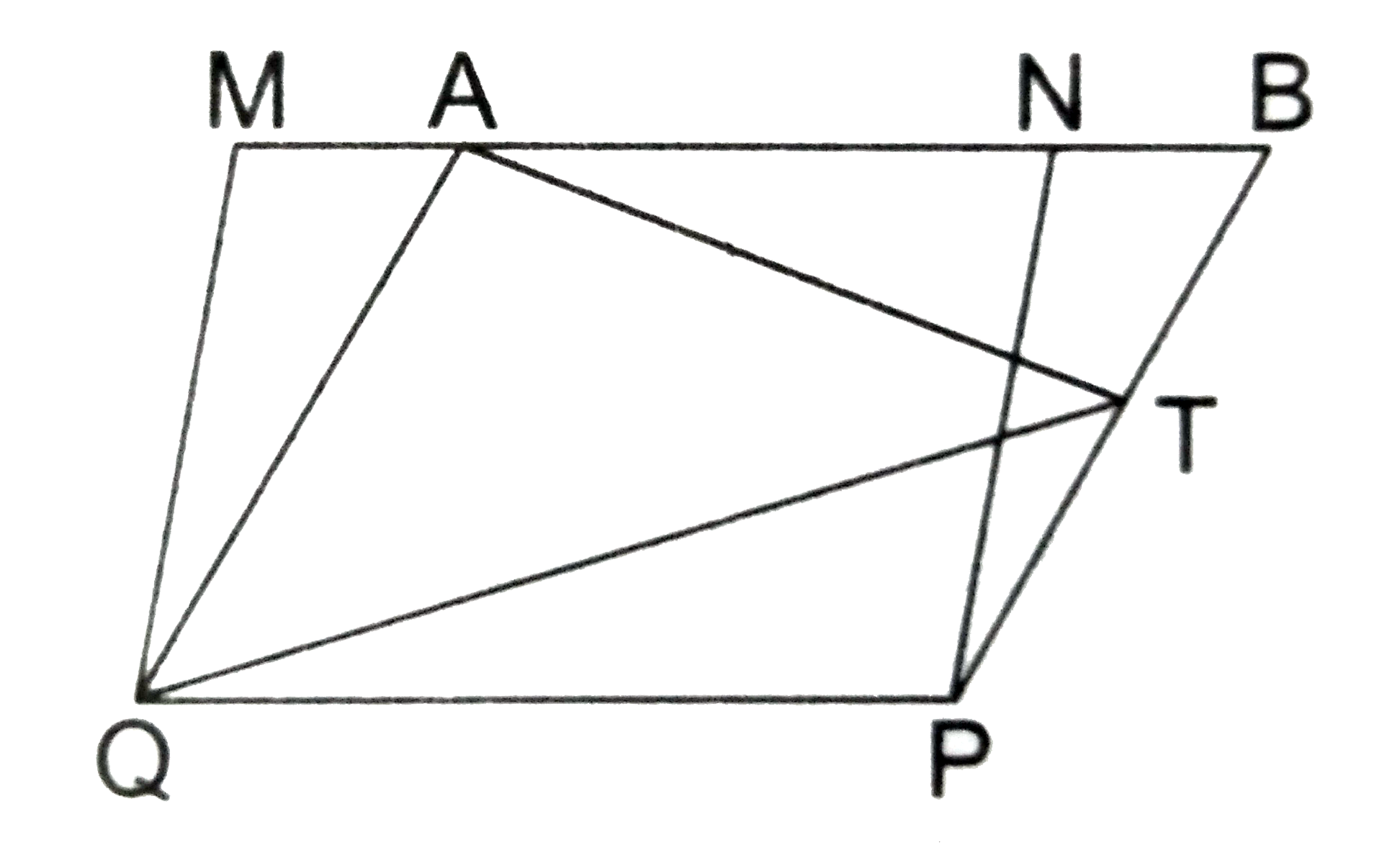
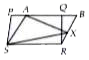
View SolutionIn the figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar(PQRS) = ar(ABRS)
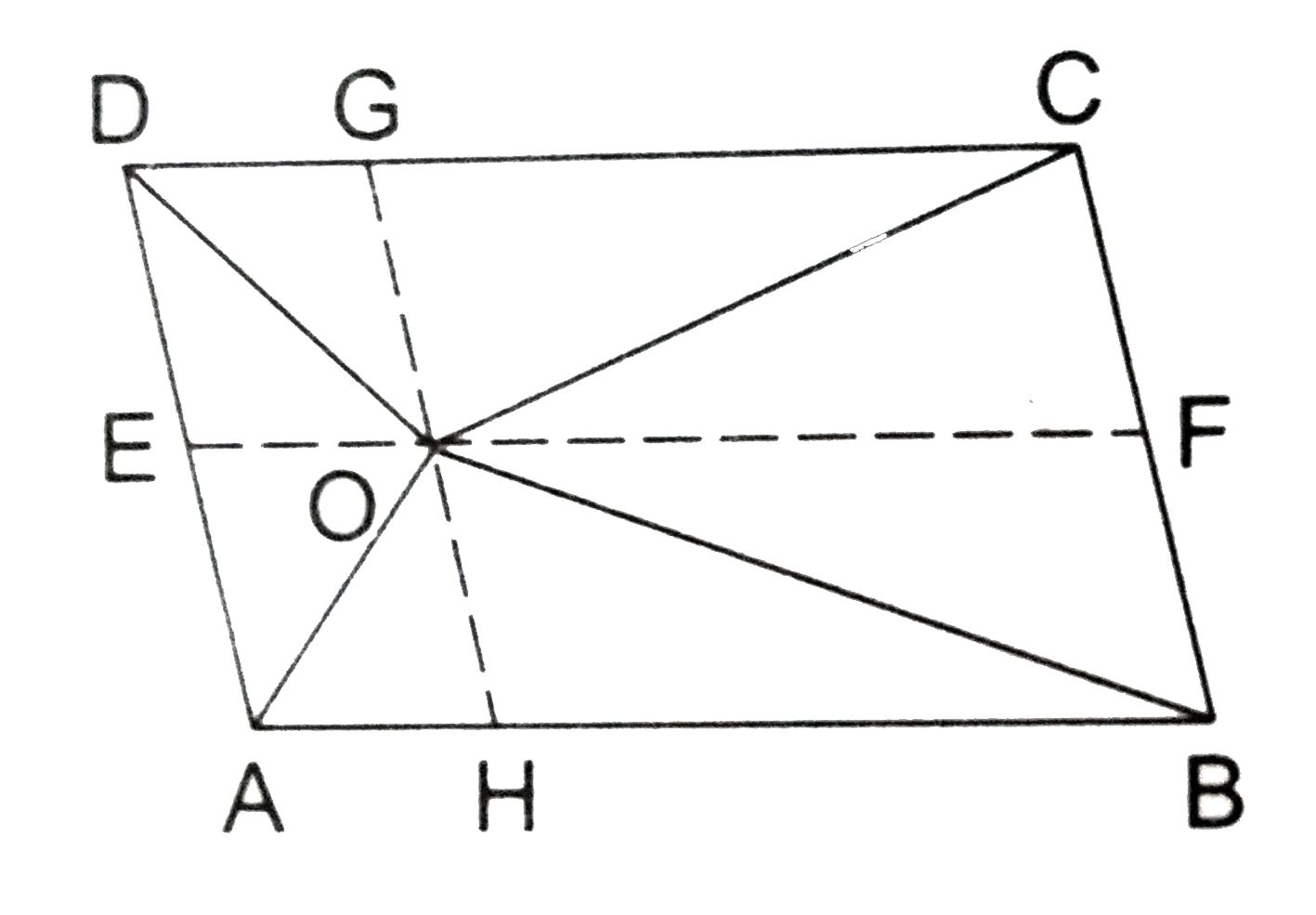
View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
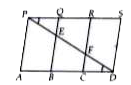
View SolutionIn the given figure PSDA is a parallelogram in which PQ =QR= RS and AP II BQ II CR II VS.Prove that ar(△PQE) = ar(△DCF).
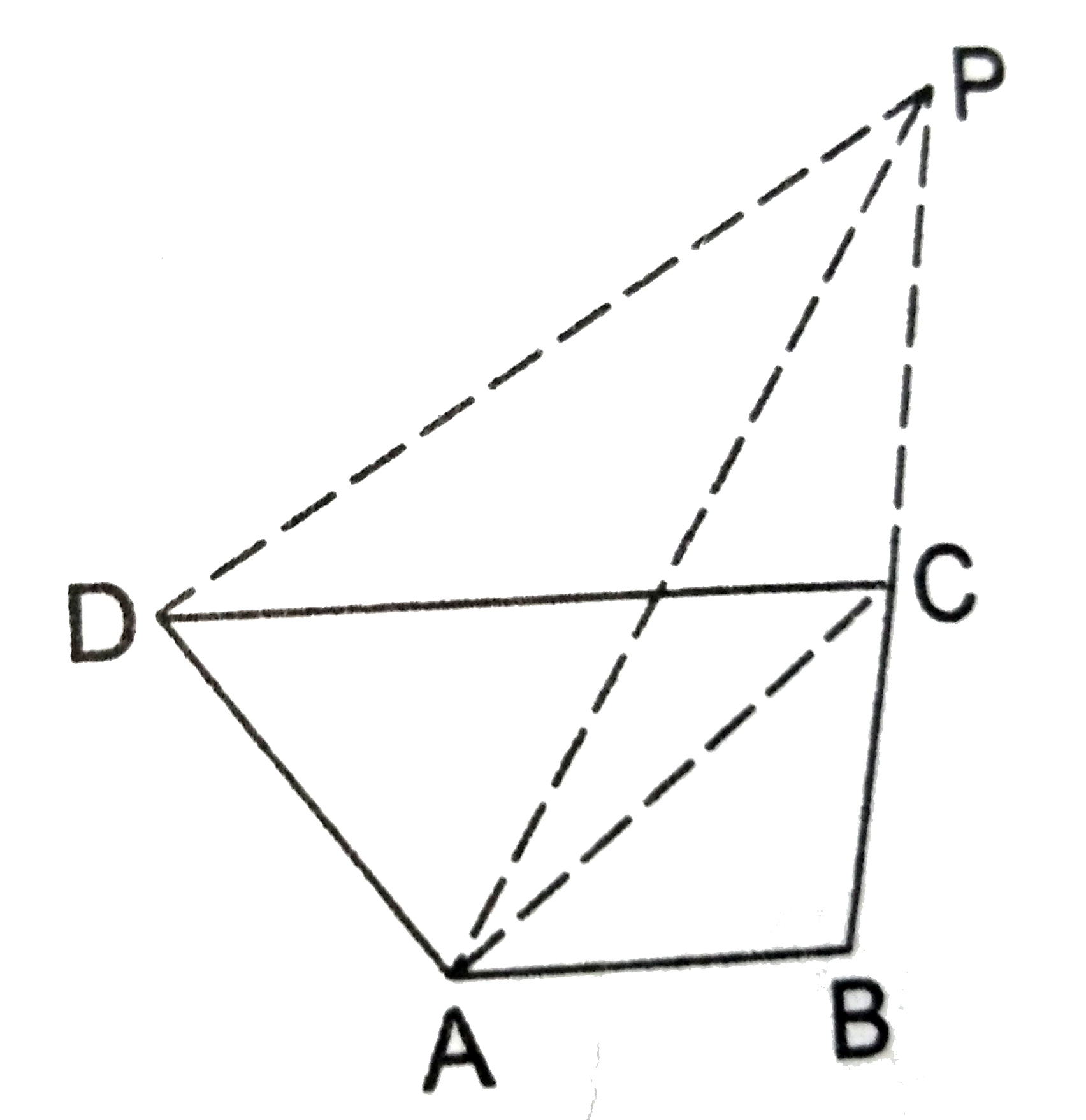
View SolutionIn the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that ar(△ABP)=ar(qaud. ABCD).
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
View Solution
