y+8≥2x
The correct Answer is:N/a
Given inequation :y+8≥2x
⇒2x−y≤8
Corresponding equation : 2x−y=8
This line cuts X-axis at A(4, 0) and Y-axis at B (0, -8)
Draw a line by joining the points A and B.
At point (0, 0), from the inequation, 0 ≤ 8 True)
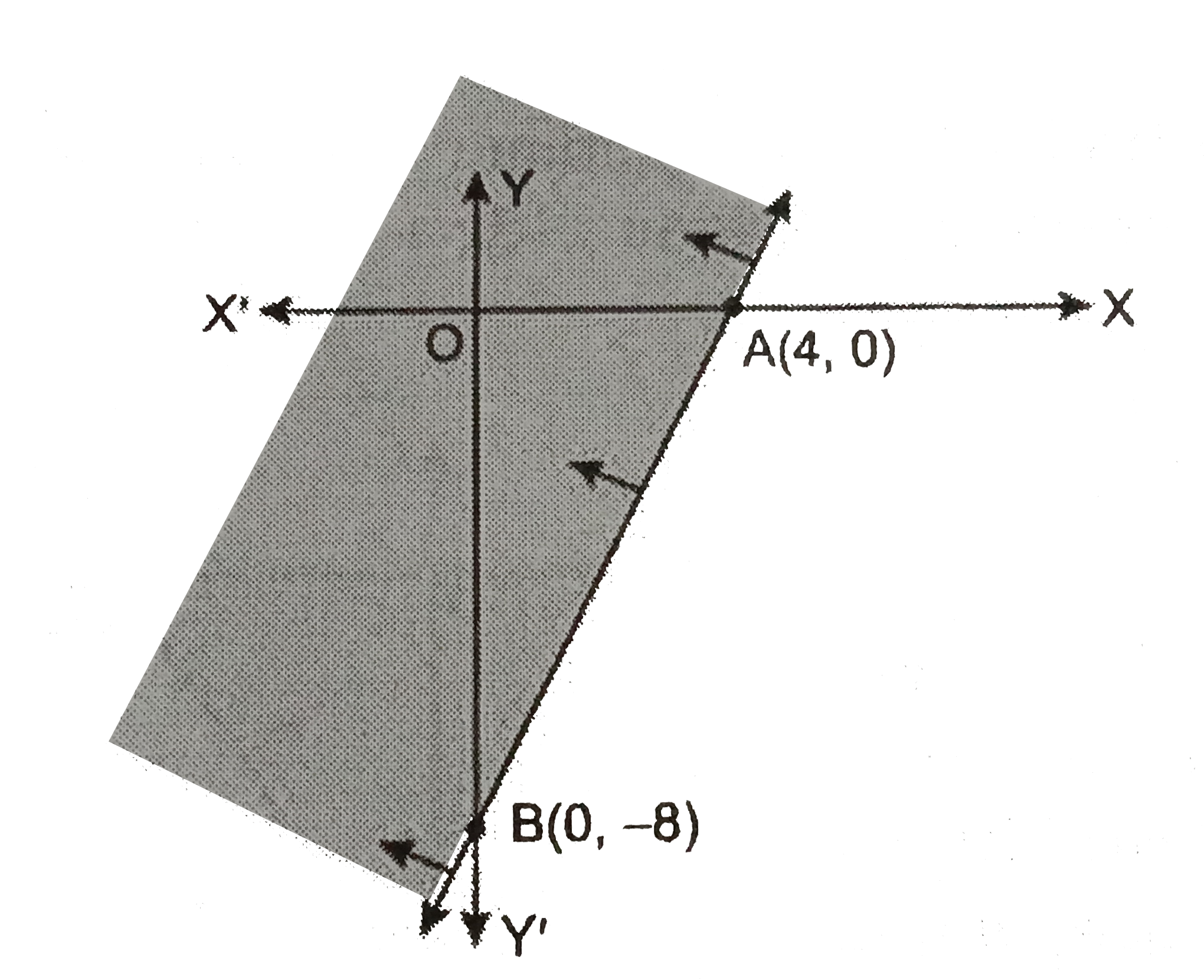
Now, shade that region of XY-plane divided by line AB in which (0, 0) lies.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR INEQUALITIESEXERCISE - MISCELLANEOUS EXERCISE14videos
LINEAR INEQUALITIES
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR INEQUALITIESEXERCISE - EXERCISE76videos
LINEAR INEQUALITIES
- BOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise30videos
LIMITS AND DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - MATHEMATICAL REASONING EXERCISE - Misellaneous exercise7videos
MATHEMATICAL REASONING
Similar Questions
Maximize z=3x+2y by graphical method Subject to
x+2y≥2
x+2y≤8
x,y≥0View SolutionZ=3x+5y
x+y≥2,x+3y≥3x≥0,y≥0View SolutionZ=3x+5y
x+3y≥3,x+y≥2,x≥0,y≥0View Solution(a) Draw the feasible region of inequation:
x+y≤4,x≥0,y≥0
(b) Draw the graph of the following LPP:
3x+y≤17,x,y≥0
(c) Shade the feasible region of LLP:
(i) x+3y≥3,x+y≥2,x≥0,y≥0
(ii) x+2y≤8,3x+2y≤12,x≥0,y≥0View SolutionMaximize z=4x+5y, subject to
2x+y≥7,2x+3y≤15,x≤3,x≥0,y≥0View SolutionDetermine graphically the minimum value of the objective function z = - 50x + 20 y, subject to he constraints.
2x−y≥−5
3x+y≥3
2x−3y≤12
x≥0,y≥0View Solution2x+y≥8,x+2y≥10
View SolutionZ=15x+30y
x+y≤8,2x+y≥8,x−2y≥0,x,y≥0View SolutionMinimize Z=2x+3y subject to constraints x+y≥6,2x+y≥7,x+4y≥8,x≥0,y≥0
View Solution2x+y≥2,x−y≤1,x+2y≤8,x≥0,y≥0.
View Solution

