A toy company manufactures two types of dolls A and B. Market research and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of Rs. 12 and Rs. 16 per doll respectively on dolls A and B how many of each should be produced weekly in order to maximise the profit?
Let the company makes x dolls of type A and y dolls to type B.
∴ Maximise Z=12x+16y
x≥0,y≥0……………. 1
x+y≤1200…………….2
y≤x/2⇒x−2y≥0……………3
x≤3y+600⇒x−3y≤600……………….4
First, draw the graph of the line x+y=1200
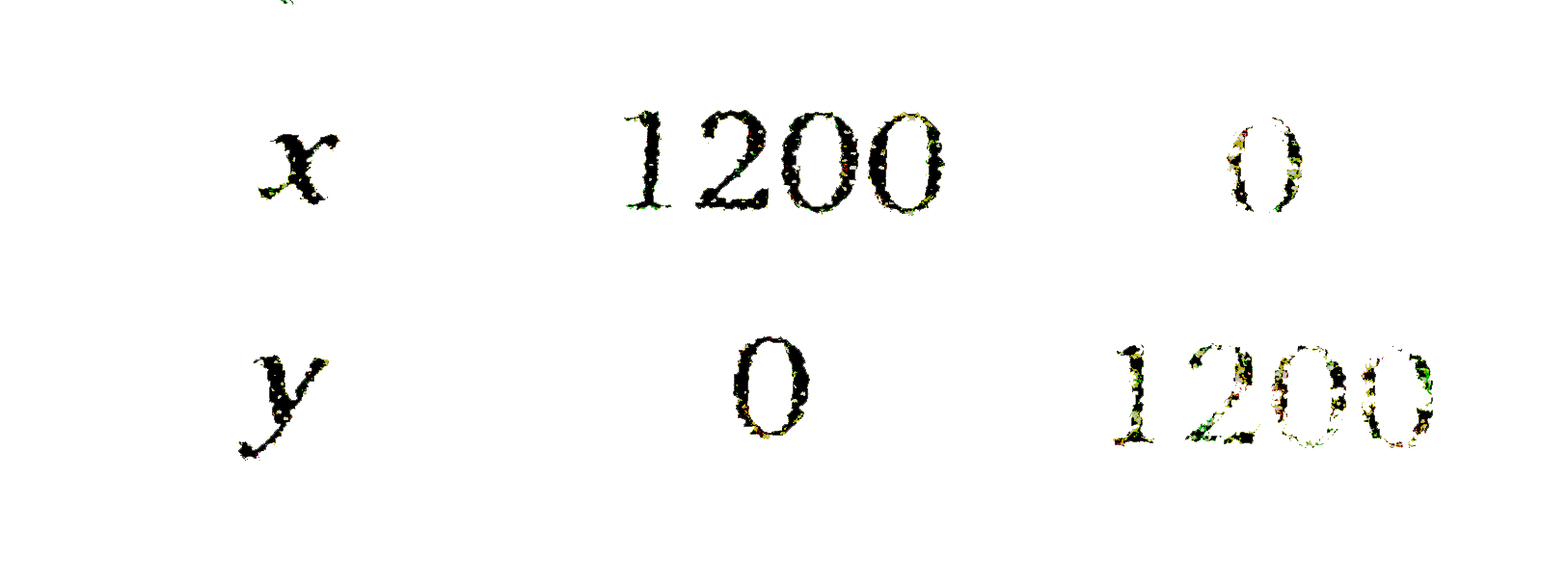
Put (0,0) in the inequation x+y≤1200,
0+≤1000⇒0≤1200 (True)
Thus, the half plane contains the origin.
Now, draw the graph of the line x−2y=0.
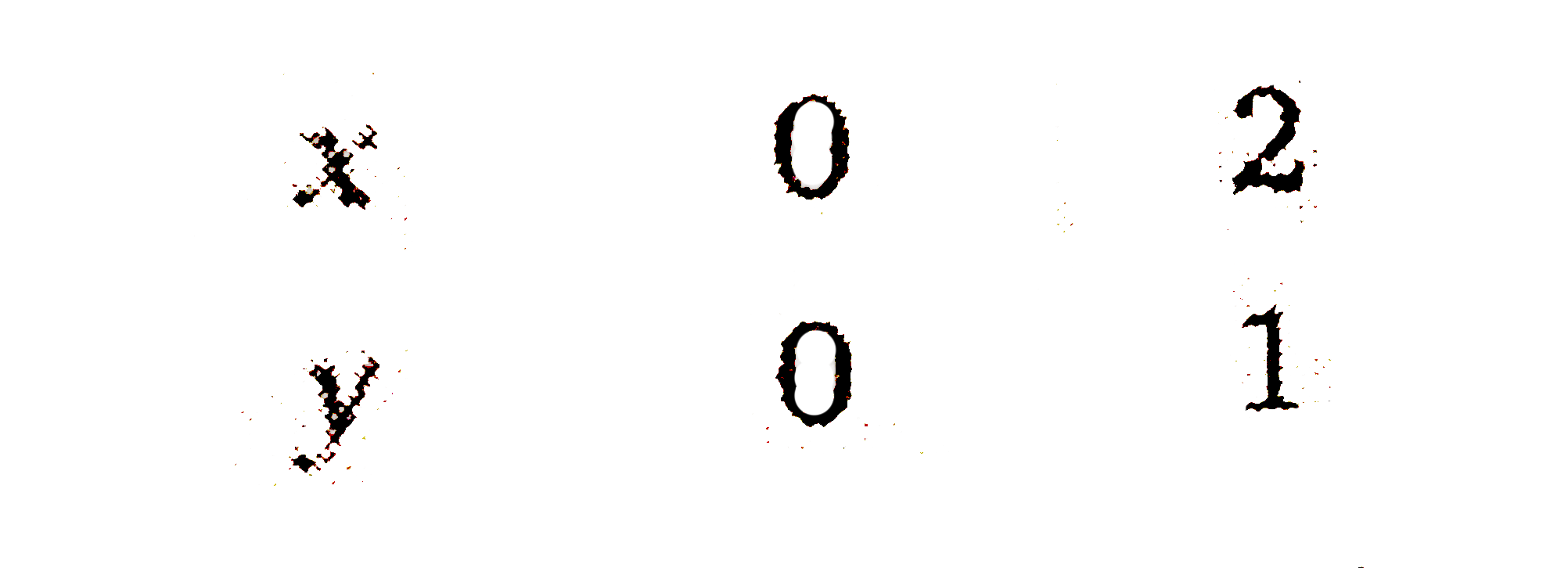
Put (200,0) in the ineuation x−2y>0,
2002x0≥0⇒200≥0 (True)
Therefore, half plane is on the side of x-axis.
Now, draw the graph of the line x−3y=600.
Put (0,0) in the inequation x−3y≤600
0+3×0≤600⇒0≤600 (True)
Thus, the half plane contains the origin.
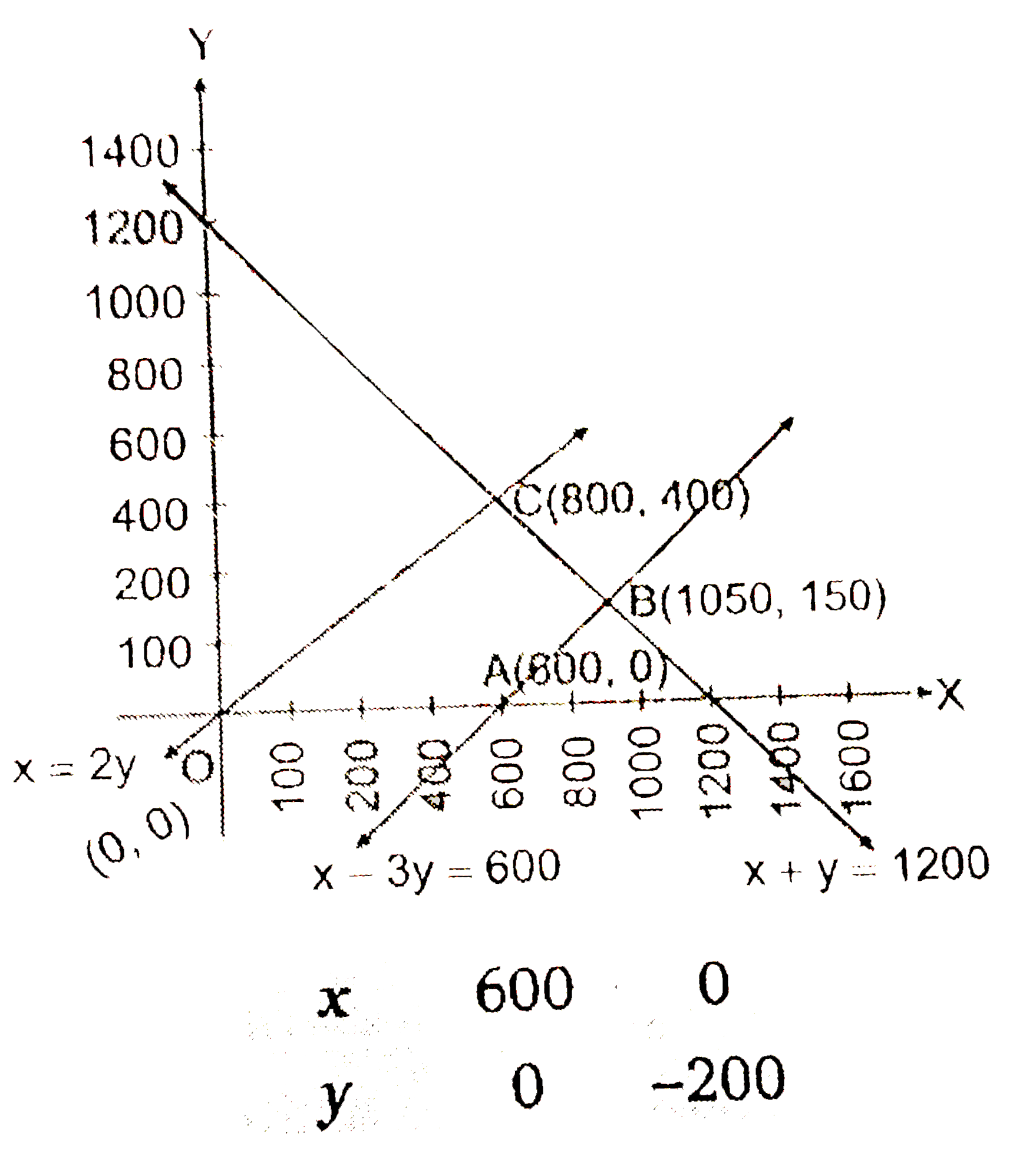
Since x,y≥0. So, the feasible region is in first quadrant.
The point of intersection of the lines x−3y=600 and x+y=1200 is B(1050,150) and for the lines x=2y and x+y=1200 is C(800,400).
∴ Feasible region is OABCO.
The vertices of the feasible region are A(600,0),B(1050,150) and C(800,400). We find the value of Z at these vertices.
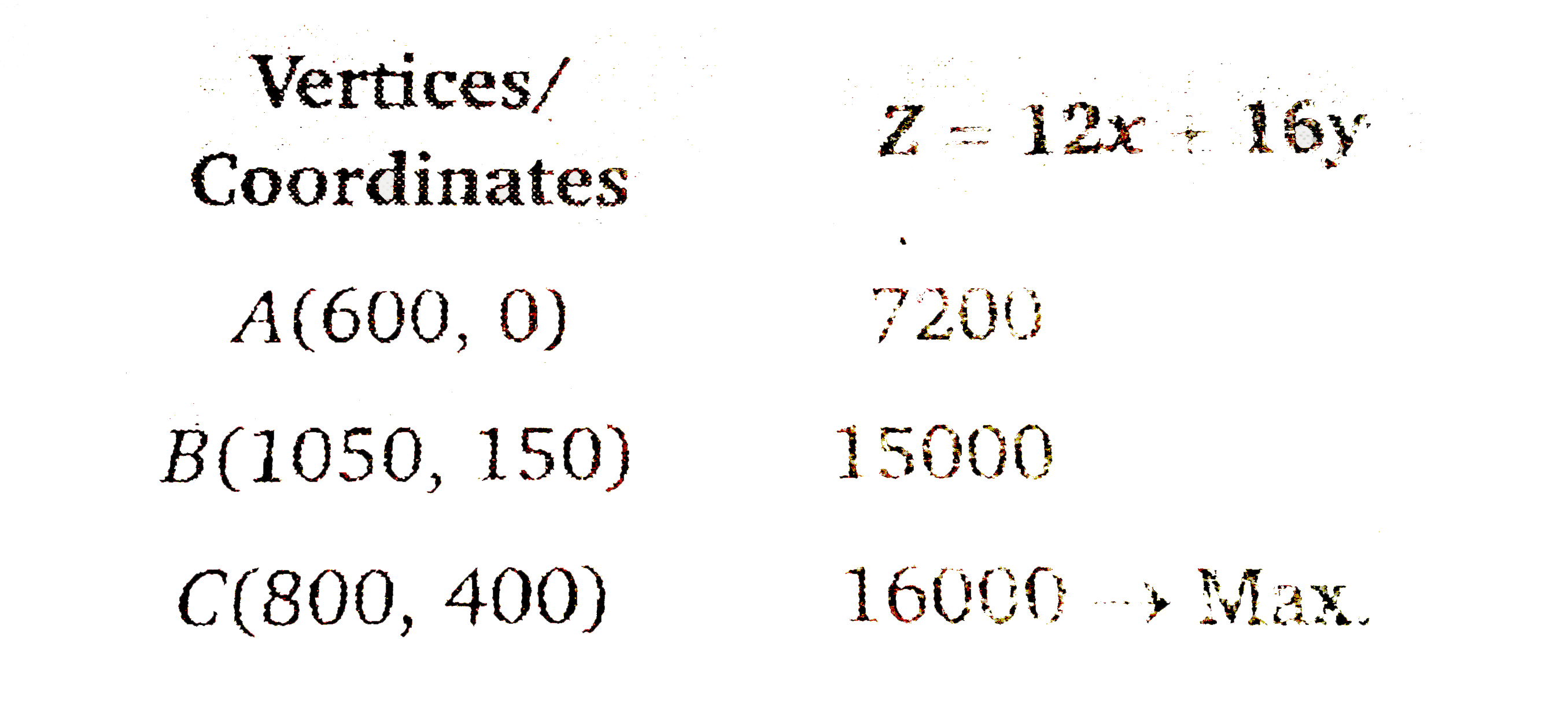
Maximum value of Z is 16000 at C(800,400).
Therefore, to obtain maximum profit of Rs. 16000, 800 dolls of type A and 400 dolls of type B should be produced.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.2
11 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of Rs 12 and Rs 16 per doll respectively on dolls A and B. how many of each should be produced weekly in order to maximise the profit?
View SolutionA toy company manufacutes two types of dolls, A and B. Each doll of type B takes twice as long to produce as one of type. A and the company would have time to make a maxium of 2000 prr day, if it produces only type.A the supply of plastic is sufficient to produce 1500 dolls per day (both A and B combined). Type B requires a fancy dress of which there are only 600 per day available. If the company makes profits of Rs.3 and Rs5 per doll respectively on dolls A and B, how many of each should be produced per day in order to mazimize the profit? Also, find the maximum profit.
View SolutionA toy manufacturer produces two types of dolls; a basic version doll A and a deluxe version doll B. Each doll of type B takes twice as long to produce as one doll of type A. The company have time to make a maximum of 2000 dolls of type A per day, the supply of plastic is sufficient to produce 1500 dolls per day and each type requires equal amount of it. The deluxe version i.e. type B requires a fancy dress of which there are only 600 per day available. If the company makes a profit of RLs. 3 and Rs. 5 per doll, respectively, on doll A and B; how many of each should be produced per day in order to maximize profit? Solve it by graphical method.
View SolutionA toy company manufactures two types of doll; a basic version doll; a basic version doll A and a deluxe version doll B. Each doll of type B takes twice as long to produce as one of type. A and the company would have time to ,make a maximum of 2, 000 per day if it produces only the basic version. The supply of plastic is sufficient to produce 1500 dolls per day (both A and B combined). The deluxe version requires a fancy dress of which there are only 600 per day available. If the company makes profit Rs. 3 and Rs. 5 per doll respectively o doll A and doll B; how many of each should be produced per day in order to maximize profit?
View SolutionA toy company manufactures two types of doll; a basic version doll; a basic version doll A and a deluxe version doll B. Each doll of type B takes twice as long to produce as one of type. A and the company would have time to ,make a maximum of 2, 000 per day if it produces only the basic version. The supply of plastic is sufficient to produce 1500 dolls per day (both A and B combined). The deluxe version requires a fancy dress of which there are only 600 per day available. If the company makes profit Rs. 3 and Rs. 5 per doll respectively o doll A and doll B; how many of each should be produced per day in order to maximize profit?
View SolutionIf 17 dolls cosr Rs306 , what do 29 dolls cost?
View SolutionA company manufactures two types of sweaters :type A sweaters type B.It costs Rs 360 to make a type A sweater and Rs 120 to make a type B sweater.The company can make at most 300 sweaters and spend at most Rs72,000 a day.The number of sweaters of type A cannot exceed the number of sweaters of type B by more than 100.The company makes a profit of Rs 200 for each sweater of type A and Rs 20 for every sweater of type B.What is the maximum profit (in Rs.)?
View SolutionName the type of type of manufacturing industry wherein two or more ingredients are combined into one products.
View SolutionA company manufacutres two types of sweaters type A and type B. It costs 360 to make type A sweater and 120 to make a type B sweater. The company can make atmost 300 sweater and spent atmost 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of 200 for each sweater of type A and 120 for every sweater of type B. Formulate this problem as a LPP to maximise the profit to the company.
View SolutionA company manufacutres two types of sweaters type A and type B. It costs 360 to make type A sweater and 120 to make a type B sweater. The company can make atmost 300 sweater and spent atmost 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of 200 for each sweater of type A and 120 for every sweater of type B. Formulate this problem as a LPP to maximise the profit to the company.
View Solution
