If M is mass of a planet and R is its radius then in order to beco

Topper's Solved these Questions

BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - B (OBJECTIVE TYPE QUESTIONS)
26videos
GRAVITATION
BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
52videos
GRAVITATION
BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - EXERCISE
20videos
GRAVITATION
BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
BOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10videos
KINETIC THEORY

Knowledge Check

Question 1 - Select One
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than $1.4$ times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius $R_{S}$ , called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius $R_{S}$ . So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about $6$ light years. that orbits this massive object with an orbital speed of about $2 \times 10^{5} m / s$ . Use the given data whereever necessary and answer the questions that hollow. $G = 6.67 \times 10^{- 11} N - m^{2} / k g^{2}$ , Solar mass $M = 2 \times 10^{30} k g, C = 3 \times 10^{8} m / s, 1$ light year $= 9.5 \times 10^{15} m$ .

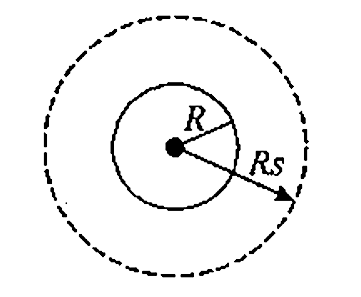
If mass of earth $M_{E} \approx 6 \times 10^{24} k g$ and its radius $R_{E} = 6400 k m$ , to what fraction of its presents radius does the earth need to be compressed in order to become a black hole ?
(Give only the order of your answer)
A $10^{- 4}$
B $10^{- 9}$
C $10^{- 7}$
D $10^{- 14}$
Question 2 - Select One
A satellite of mass m goes round the earth along a circular path of radius r. Let $m_{E}$ be the mass of the earth and $R_{E}$ its radius then the linear speed of the satellite depends on.
A $m, m_{E}$ and $r$
B $m, R_{E}$ and $r$
C $m_{E}$ only
D $m_{E}$ and $r$
Question 3 - Select One
Consider a hypothetical planet which is very long and cylinderical. The density of the planet is $ρ$ , its radius is $R$ .

What is the possible orbital speed of the satellite in moving around the planet in circular orbit in a plane which is perpendicular to the axis of planet?
A $R \sqrt{π G ρ}$
B $2 R \sqrt{π G ρ}$
C $R \sqrt{2 π G ρ}$
D $R \sqrt{\frac{G ρ}{2 π}}$

If M is mass of a planet and R is its radius then in order to become black hole [ c is speed of light ]

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

A satellite of mass m goes round the earth along a circular path of radius r. Let $m_{E}$ be the mass of the earth and $R_{E}$ its radius then the linear speed of the satellite depends on.

Consider a hypothetical planet which is very long and cylinderical. The density of the planet is $ρ$ , its radius is $R$ .

What is the possible orbital speed of the satellite in moving around the planet in circular orbit in a plane which is perpendicular to the axis of planet?

AAKASH INSTITUTE-GRAVITATION -ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)

If M is mass of a planet and R is its radius then in order to become black hole [ c is speed of light ]

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

A satellite of mass m goes round the earth along a circular path of radius r. Let mE be the mass of the earth and RE its radius then the linear speed of the satellite depends on.

Consider a hypothetical planet which is very long and cylinderical. The density of the planet is ρ, its radius is R. What is the possible orbital speed of the satellite in moving around the planet in circular orbit in a plane which is perpendicular to the axis of planet?

AAKASH INSTITUTE-GRAVITATION -ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)

A satellite of mass m goes round the earth along a circular path of radius r. Let $m_{E}$ be the mass of the earth and $R_{E}$ its radius then the linear speed of the satellite depends on.

Consider a hypothetical planet which is very long and cylinderical. The density of the planet is $ρ$ , its radius is $R$ .

What is the possible orbital speed of the satellite in moving around the planet in circular orbit in a plane which is perpendicular to the axis of planet?