An artificial satellite relolves around a planet for which gravitational force (F) varies with distance r from its centres as If its orbital speed , then
The correct Answer is:B
To solve the problem step by step, we will analyze the relationship between the gravitational force acting on the satellite and its orbital speed.
1. Understanding the Gravitational Force:
The problem states that the gravitational force F varies with distance r from the center of the planet as:
F∝r2
This means we can express the gravitational force as:
F=k⋅r2
where k is a constant of proportionality.
2. Centripetal Force Requirement:
For a satellite in circular motion, the gravitational force provides the necessary centripetal force to keep the satellite in orbit. The centripetal force Fc is given by:
Fc=mv20r
where m is the mass of the satellite and v0 is its orbital speed.
3. Equating Forces:
Since the gravitational force is providing the centripetal force, we can set the two forces equal to each other:
k⋅r2=mv20r
4. Rearranging the Equation:
To find an expression for v20, we can rearrange the equation:
k⋅r3=mv20
Thus, we can express v20 as:
v20=km⋅r3
5. Finding Orbital Speed:
Taking the square root of both sides gives us the expression for the orbital speed v0:
v0=√km⋅r3/2
6. Identifying the Relationship:
Since km is a constant, we can express v0 in terms of r:
v0∝r3/2
This indicates that the orbital speed v0 varies with the distance r from the center of the planet as r3/2.
Conclusion:
The correct relationship is:
v0∝r3/2
The problem states that the gravitational force F varies with distance r from the center of the planet as:
F∝r2
This means we can express the gravitational force as:
F=k⋅r2
where k is a constant of proportionality.
For a satellite in circular motion, the gravitational force provides the necessary centripetal force to keep the satellite in orbit. The centripetal force Fc is given by:
Fc=mv20r
where m is the mass of the satellite and v0 is its orbital speed.
Since the gravitational force is providing the centripetal force, we can set the two forces equal to each other:
k⋅r2=mv20r
To find an expression for v20, we can rearrange the equation:
k⋅r3=mv20
Thus, we can express v20 as:
v20=km⋅r3
Taking the square root of both sides gives us the expression for the orbital speed v0:
v0=√km⋅r3/2
Since km is a constant, we can express v0 in terms of r:
v0∝r3/2
This indicates that the orbital speed v0 varies with the distance r from the center of the planet as r3/2.
The correct relationship is:
v0∝r3/2
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - B (OBJECTIVE TYPE QUESTIONS)
26 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
52 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - EXERCISE
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
The mass density of a planet of radius R varie with the distance r form its centre as ρ(r)=p0(1−r2R2). Then the graviational field is maximum at :
View SolutionAssume that the force of gravitation F∝1rn . Then show that the orbital speed in a circular orbit of radius r is proportional to 1r(n−1)/2 , while its period T is proportional to r(n+1)/2
View Solution
Knowledge Check
Natural or artificial bodies that revolve around a planet under its gravitational force of attraction are called
AMeteoritesBMeteorsCStarDSatellitesTwo satellite of mass m and 2 m are revolving in two circular orbits of radius r and 2r around an imaginary planet , on the surface of with gravitational force is inversely proportional to distance from its centre . The ratio of orbital speed of satellite is .
A1:1B1:2C2:1D1:√2A : Angular momentum of a satellite about a planet is constant .
R :Gravitational force is a central force so its torque about the sun is zero .AIf both Assertion & Reason are true . And the reason is the correct explanation of the assertion , then mark (1)BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion , then mark (2)CIf Assertion is true statement but Reason is false , then mark (3)DIt will move the same speed , tangentially to the spacecraft
In a spherical region the densiy varies inversely with the distance from ther centre Gravitational field at a distance r from the centre is .
View SolutionThe orbital speed of a satellite revolving around a planet in a circular orbit is v0 . If its speed is increased by 10 % ,then
View SolutionAn artificial satellite moving in a circular orbit around the earth has a total energy E0. Its potential energy is
View SolutionA satellite moves around the earth in a circular orbit with speed v. If m is the mass of the satellite, its total energy is
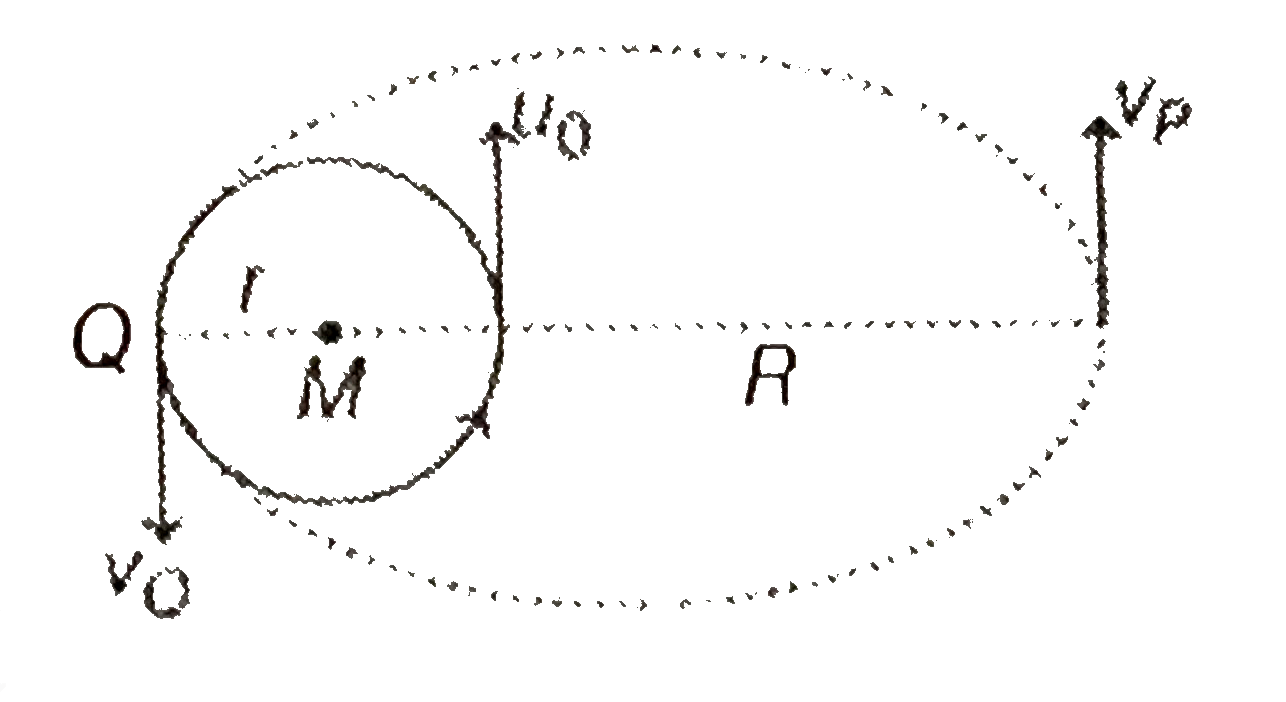
View SolutionA light satellite is initially rotating around a planet in a circular orbit of radius r. Its speed in this circular orbit was u0. It is put in an elliptical orbit by increasing its speed form u0 to vQ ( instantaneously). In the elliptical orbit, the satellite reaches the farthest point P, which is at a distance R from the planet. Satellite's speed at farthest point is vP. At point Q, the speed required by satellite to escape the planet's gravitational pull is vesc
View Solution
