Question

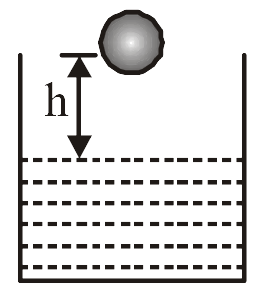
A ball of density o and radius r is dropped on the surface of a liquid of density p from certain height. If speed of ball does not change even on entering in liquid and viscosity of liquid is r). then the height from which ball dropped is

Options

A. `2g [(((sigma - rho)r)^(2))/(9eta)]`
B. `(2g (sigma - rho)^(2) r^(2))/(9eta)`
C. `(2 (sigma - rho)^(2) gr^(2))/(9eta)`
D. `2g [(9eta)/(((sigma - rho)r)^(2))]`

Explanation

To solve the problem step by step, we will analyze the forces acting on the ball and use the principles of energy conservation and fluid mechanics.

Step 1: Understand the Problem
We have a ball of density \( \sigma \) and radius \( r \) that is dropped from a height \( h \) into a liquid of density \( \rho \). The ball reaches a constant speed upon entering the liquid, indicating that the net force acting on it is zero.

Step 2: Apply Conservation of Energy
When the ball is dropped from height \( h \), it has gravitational potential energy given by:
\( PE = mgh \)
where \( m \) is the mass of the ball, \( g \) is the acceleration due to gravity, and \( h \) is the height from which it is dropped.

As the ball enters the liquid and reaches a constant speed \( v \), all the potential energy converts into kinetic energy:
\( KE = \frac{1}{2} mv^2 \)
Setting these equal gives us:
\( mgh = \frac{1}{2} mv^2 \)

Step 3: Simplify the Equation
We can cancel \( m \) from both sides (assuming \( m \neq 0 \)):
\( gh = \frac{1}{2} v^2 \)
Rearranging gives:
\( h = \frac{v^2}{2g} \)
This will be our Equation (1).

Step 4: Analyze Forces Acting on the Ball in the Liquid
When the ball is submerged in the liquid, it experiences three forces:
1. Weight of the ball \( W = mg = \frac{4}{3} \pi r^3 \sigma g \)
2. Buoyant force \( F_b = \text{Weight of liquid displaced} = \frac{4}{3} \pi r^3 \rho g \)
3. Drag force \( F_d \) due to viscosity, given by Stokes' law:
\( F_d = 6 \pi r \eta v \)

Step 5: Set Up the Force Balance
Since the ball moves with constant velocity, the net force is zero:
\( mg = F_b + F_d \)
Substituting the expressions for weight, buoyant force, and drag force:
\( \frac{4}{3} \pi r^3 \sigma g = \frac{4}{3} \pi r^3 \rho g + 6 \pi r \eta v \)

Step 6: Rearranging the Equation
Rearranging gives:
\( \frac{4}{3} \pi r^3 \sigma g - \frac{4}{3} \pi r^3 \rho g = 6 \pi r \eta v \)
Factoring out common terms:
\( \frac{4}{3} \pi r^3 g (\sigma - \rho) = 6 \pi r \eta v \)
Dividing both sides by \( \pi \):
\( \frac{4}{3} r^2 g (\sigma - \rho) = 6 \eta v \)
Solving for \( v \):
\( v = \frac{2}{9} \frac{r^2 g (\sigma - \rho)}{\eta} \)

Step 7: Substitute \( v \) Back into Equation (1)
Now substituting \( v \) back into our height equation:
\( h = \frac{v^2}{2g} = \frac{1}{2g} \left(\frac{2}{9} \frac{r^2 g (\sigma - \rho)}{\eta}\right)^2 \)
Calculating \( v^2 \):
\( v^2 = \left(\frac{2}{9} \frac{r^2 g (\sigma - \rho)}{\eta}\right)^2 = \frac{4}{81} \frac{r^4 g^2 (\sigma - \rho)^2}{\eta^2} \)
Substituting this back into the height equation:
\( h = \frac{1}{2g} \cdot \frac{4}{81} \frac{r^4 g^2 (\sigma - \rho)^2}{\eta^2} \)
This simplifies to:
\( h = \frac{2 r^4 (\sigma - \rho)^2 g}{81 \eta^2} \)

Final Result
Thus, the height from which the ball is dropped is:
\( h = \frac{2 r^2 (\sigma - \rho) g}{9 \eta} \)