A ball is dropped from height h. If falls on liquid surface. Its velocity does not change when its enters in liquid. Find height h in terms of r = radius of ball, σ = density of liquid, ρ = density of ball η = coefficient of viscosity and g = acceleration due to gravity :
2r4g(ρ−σ)281η2
2r4g(ρ−σ)250η2
2r4g(ρ−σ)225η2
2r4g(ρ−σ)290η2
The correct Answer is:A
To solve the problem, we need to find the height h from which a ball is dropped, given that its velocity does not change when it enters a liquid. We will use the concepts of free fall and terminal velocity.
1. Determine the velocity of the ball just before it enters the liquid:
The ball is dropped from height h. Using the equation of motion for free fall:
v=√2gh
where v is the velocity of the ball just before it hits the liquid, g is the acceleration due to gravity, and h is the height.
2. Identify the terminal velocity:
When the ball enters the liquid, it reaches a terminal velocity Vt. The formula for terminal velocity Vt of a sphere moving through a viscous fluid is given by:
Vt=29(ρ−σ)gr2η
where:
- ρ is the density of the ball,
- σ is the density of the liquid,
- r is the radius of the ball,
- η is the coefficient of viscosity.
3. Set the velocities equal:
According to the problem, the velocity of the ball just before it enters the liquid is equal to the terminal velocity when it is in the liquid:
√2gh=Vt
4. Substitute the expression for terminal velocity:
Substituting the expression for Vt into the equation gives:
√2gh=29(ρ−σ)gr2η
5. Square both sides to eliminate the square root:
Squaring both sides results in:
2gh=(29(ρ−σ)gr2η)2
6. Simplify the equation:
Expanding the right-hand side:
2gh=481(ρ−σ)2g2r4η2
7. Cancel g from both sides:
Dividing both sides by g (assuming g≠0):
2h=481(ρ−σ)2gr4η2
8. Solve for h:
Rearranging gives:
h=281(ρ−σ)2gr4η2
Final Expression:
Thus, the height h in terms of r, σ, ρ, η, and g is:
h=281(ρ−σ)2gr4η2
The ball is dropped from height h. Using the equation of motion for free fall:
v=√2gh
where v is the velocity of the ball just before it hits the liquid, g is the acceleration due to gravity, and h is the height.
When the ball enters the liquid, it reaches a terminal velocity Vt. The formula for terminal velocity Vt of a sphere moving through a viscous fluid is given by:
Vt=29(ρ−σ)gr2η
where:
- ρ is the density of the ball,
- σ is the density of the liquid,
- r is the radius of the ball,
- η is the coefficient of viscosity.
According to the problem, the velocity of the ball just before it enters the liquid is equal to the terminal velocity when it is in the liquid:
√2gh=Vt
Substituting the expression for Vt into the equation gives:
√2gh=29(ρ−σ)gr2η
Squaring both sides results in:
2gh=(29(ρ−σ)gr2η)2
Expanding the right-hand side:
2gh=481(ρ−σ)2g2r4η2
Dividing both sides by g (assuming g≠0):
2h=481(ρ−σ)2gr4η2
Rearranging gives:
h=281(ρ−σ)2gr4η2
Thus, the height h in terms of r, σ, ρ, η, and g is:
h=281(ρ−σ)2gr4η2
Topper's Solved these Questions
Similar Questions
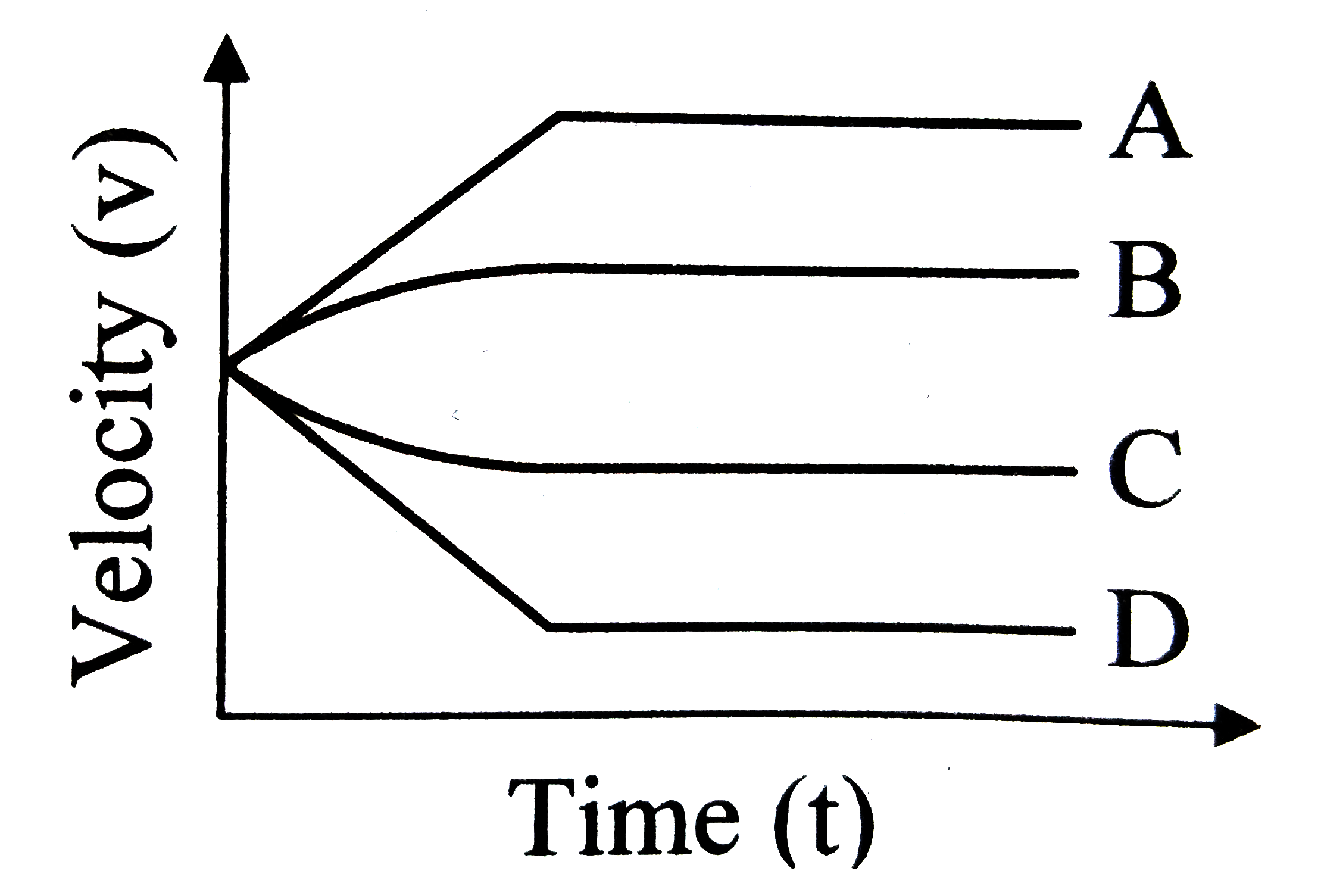
A small spherical solid ball is dropped from a great height in a viscous liquid . Its journey in the liquid is best described in the diagram given below by the
View SolutionA ball weighs 80 g in air 60g in water and 50g in liquid if the density of water is 1gcm−3 find the density of this liquid.
View Solution
Knowledge Check
The absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
AρghBPa+ρghCPa−ρghDPa2ρghA small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
ASHMBperiodic but not SHMCnot periodicDSHM for half a period and non-periodic for rest half of the periodA small ball is dropped in a viscous liquid. Its fall in the liquid is best described by the figure
 Acurve ABcurve BCcurve CDcurve D
Acurve ABcurve BCcurve CDcurve D
A ball of density o and radius r is dropped on the surface of a liquid of density p from certain height. If speed of ball does not change even on entering in liquid and viscosity of liquid is r). then the height from which ball dropped is
View SolutionA ball is dropped from a height h onto a floor and rebounds to a height h/6. The coefficient of restitution between the ball and the floor is
View SolutionA ball of density ρ is dropped from a height on the suraca of a non-visous liquid of dinsity 2ρ. Choose the correct options.

View SolutionAssertion: A ball is dropped from a certain height above the free suface of and ideal fluid. When the ball enters the liquid it mau accelerate or retard.
Reason: Ball accelerates of retards it all depends on the dinsity of ball and the density of liquid.

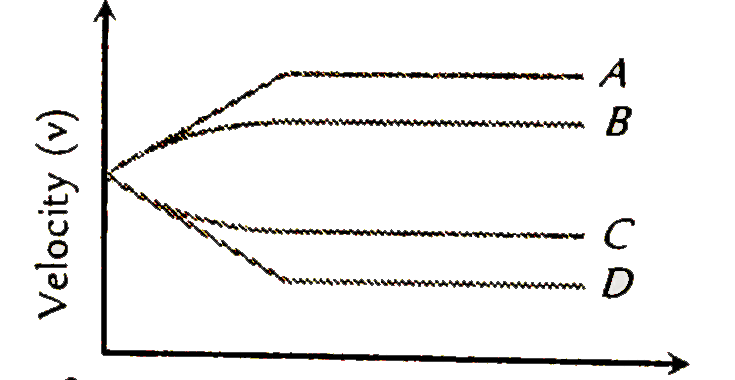
View SolutionA small spherical solid ball is dropped from a great height in a viscous liquid. Its journey in the liquid is best described in the diagram given below by the
View Solution
