Question

If an object at absolute temperature (1) radiates energy at rate R, then select correct graph showing the variation of ${\log }_e$ R with ${\log }_e$ (T).

Options

A.
B.
C.
D.

Explanation

To solve the problem of determining the correct graph showing the variation of $${\log }_{e}R$$ with $${\log }_{e}T$$, we will follow these steps:

1. Understand the relationship: According to Stefan-Boltzmann law, the rate of energy radiation \( R \) from a body is proportional to the fourth power of its absolute temperature \( T \). This can be expressed mathematically as:
\( R = \sigma \cdot A \cdot T^4 \)
where \( \sigma \) is the Stefan-Boltzmann constant and \( A \) is the surface area of the object.

2. Rearranging the equation: We can express \( R \) in terms of \( T \):
\( R = k \cdot T^4 \)
where \( k = \sigma \cdot A \) is a constant.

3. Taking logarithms: To analyze the relationship between \( R \) and \( T \), we take the natural logarithm (base \( e \)) of both sides:
\( \log_e R = \log_e (k \cdot T^4) \)

4. Applying logarithmic properties: Using the properties of logarithms, we can expand the right-hand side:
\( \log_e R = \log_e k + \log_e (T^4) \)
\( \log_e R = \log_e k + 4 \log_e T \)

5. Identifying the graph: This equation can be rearranged to fit the linear form \( y = mx + c \):
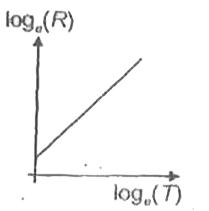
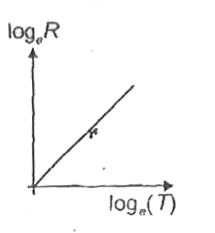
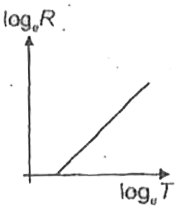
\( \log_e R = 4 \log_e T + \log_e k \)
Here, \( y = \log_e R \), \( x = \log_e T \), the slope \( m = 4 \), and the y-intercept \( c = \log_e k \).

6. Graph characteristics: Since the relationship is linear, the graph of \( \log_e R \) versus \( \log_e T \) will be a straight line with a slope of 4. The line will intersect the y-axis at \( \log_e k \) (a positive value since \( k \) is positive).

7. Conclusion: The graph will have a positive slope and will be a straight line. The correct graph that represents this relationship is the one that shows a straight line with a slope of 4.