A copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
Bωl2
32Bωl2
12Bωl2
2Bωl2
The correct Answer is:C
To find the induced e.m.f. (electromotive force) between the two ends of a copper rod of length l that is rotated about one end perpendicular to a uniform magnetic field B with a constant angular velocity ω, we can follow these steps:
1. Understanding the Setup:
- We have a copper rod of length l rotating about one end in a uniform magnetic field B.
- The rod is perpendicular to the magnetic field, and it rotates with a constant angular velocity ω.
2. Induced EMF Formula:
- The induced e.m.f. E can be calculated using Faraday's law of electromagnetic induction, which states:
E=−dΦdt
where Φ is the magnetic flux.
3. Calculating Magnetic Flux:
- The magnetic flux Φ through the area swept by the rod can be expressed as:
Φ=B⋅A
where A is the area swept by the rod as it rotates.
4. Area Swept by the Rod:
- As the rod rotates, it sweeps out a circular sector. The angle θ that the rod sweeps in time t is given by:
θ=ωt
- The area A swept by the rod at time t is:
A=12L2θ=12L2(ωt)
- Therefore, the magnetic flux becomes:
Φ=B⋅12L2(ωt)
5. Finding the Rate of Change of Flux:
- To find the induced e.m.f., we need to differentiate the magnetic flux with respect to time:
dΦdt=ddt(B⋅12L2(ωt))=B⋅12L2ω
6. Calculating Induced EMF:
- Substituting this into the e.m.f. formula gives:
E=−dΦdt=−(B⋅12L2ω)
- The negative sign indicates the direction of the induced e.m.f. according to Lenz's law, but the magnitude of the induced e.m.f. is:
E=12BL2ω
Final Answer:
The induced e.m.f. between the two ends of the copper rod is:
E=12BL2ω
- We have a copper rod of length l rotating about one end in a uniform magnetic field B.
- The rod is perpendicular to the magnetic field, and it rotates with a constant angular velocity ω.
- The induced e.m.f. E can be calculated using Faraday's law of electromagnetic induction, which states:
E=−dΦdt
where Φ is the magnetic flux.
- The magnetic flux Φ through the area swept by the rod can be expressed as:
Φ=B⋅A
where A is the area swept by the rod as it rotates.
- As the rod rotates, it sweeps out a circular sector. The angle θ that the rod sweeps in time t is given by:
θ=ωt
- The area A swept by the rod at time t is:
A=12L2θ=12L2(ωt)
- Therefore, the magnetic flux becomes:
Φ=B⋅12L2(ωt)
- To find the induced e.m.f., we need to differentiate the magnetic flux with respect to time:
dΦdt=ddt(B⋅12L2(ωt))=B⋅12L2ω
- Substituting this into the e.m.f. formula gives:
E=−dΦdt=−(B⋅12L2ω)
- The negative sign indicates the direction of the induced e.m.f. according to Lenz's law, but the magnitude of the induced e.m.f. is:
E=12BL2ω
The induced e.m.f. between the two ends of the copper rod is:
E=12BL2ω
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION - B) (OBJECTIVE TYPE QUESTIONS)
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -C) Previous Years Questions
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTEChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE
Explore 17 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTEChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION -J(Aakash Challengers Questions)
Explore 5 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTEChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
Similar Questions
A copper rod of length l rotates an angular velocity ω in a uniform magnetic field B as show in figure . What is the induced emf across its ends ?
View SolutionA copper rod AB of length l is rotated about one end A with a constant angular velocity ω. Calculate the electric field at a distance x from the axis of rotation. Also determine PD between A and B.
View Solution
Knowledge Check
A copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
A12Bωl2B34Bωl2CBωl2D2Bωl2A conducting rod is rotated about one end in a plane perpendicular to a uniform magnetic field with constant angular velocity. The correct graph between the induced emf (e) across the rod and time (t) is
A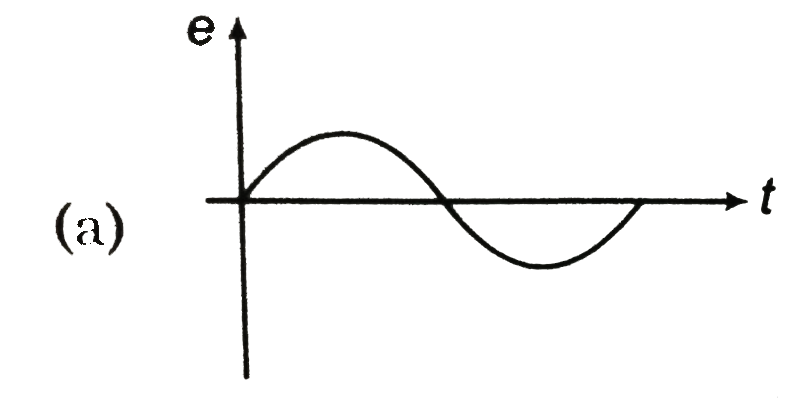 B
B C
C D
D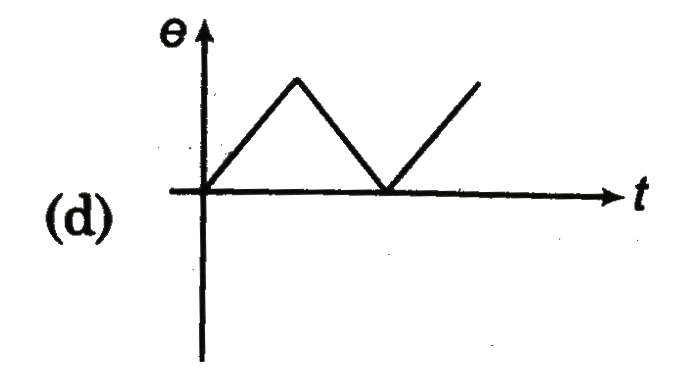
A half metre rod is rotating abou tone fixed end perpendicular to uniform magnetic field 4×10−5T with angular velocity 720 rpm. The emf induced across its ends is
A0.24 VB0.36 VC0.12 VD0.36 mV
A rod OA of length l is rotating (about end O) over a conducting ring in crossed magnetic field B with constant angular velocity ω as shown in figure.
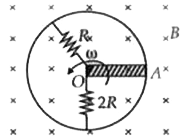
View SolutionA circular loop is kept perpendicular to a uniform magnetic field. Loop is rotated about its diameter with constant angular velocity.
View SolutionA conducing rod of length l is falling with a velocity v perpendicular to a unifrorm horizontal magnetic field B . The potential difference between its two ends will be
View SolutionA metallic rod of length l is hinged at the point M and is rotating about an axis perpendicular to the plane of paper with a constant angular velocity ω. A uniform magnetic field of intensity B is acting in the region (as shown in the figure) parallel to the plane of paper. The potential difference between the points M and N

View Solutiona semicircle wire of radius R is rotated with constant angular velocity about an axis passing through one end and perpendicular to the plane of wire. There is a uniform magnetic field of strength B. The induced emf between the ends is

View Solution
