A rod OA of length l is rotating (about end O) over a conducting ring in crossed magnetic field B with constant angular velocity ω as shown in figure.
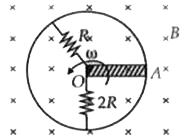
Current flowing through the rod is 3Bωl24R
Magnetic force acting on the rod is 3B2ωl34R
Torque due to magnetic force acting on the rod is 3B2ωl48R
Magnitude of external force that acts perpendicularly at the end of the rod of maintain the constant angular speed is 3B2ωl38R
The correct Answer is:A, B, C, D
I=ε2R3=3ε2R=32R×12Bωl2=3Bωl24R
Magnetic force
F=3Bωl24R×l×B=3B2ωl34R
Torque, τ=3B2ωl34R×l2=3B2ωl48R
∴ Force to be applied at the end =3B2ωl38R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT BOOK - MTG-WBJEECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT EXERCISE - WB JEE Previous Years Questions
14 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT BOOK - MTG-WBJEECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT EXERCISE - WB JEE WORKOUT (Category 2 : Single Option Correct Type)
15 Videos
- CURRENT ELECTRICITY BOOK - MTG-WBJEECHAPTER - CURRENT ELECTRICITY EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
21 Videos
- ELECTROMAGNETIC WAVES BOOK - MTG-WBJEECHAPTER - ELECTROMAGNETIC WAVES EXERCISE - WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
10 Videos
Similar Questions
A copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View SolutionA copper rod of length l is rotated about one end perpendicular to the magnetic field B with constant angular velocity ω . The induced e.m.f between the two ends is
View Solution
Knowledge Check
A copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
ABωl2B32Bωl2C12Bωl2D2Bωl2A copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
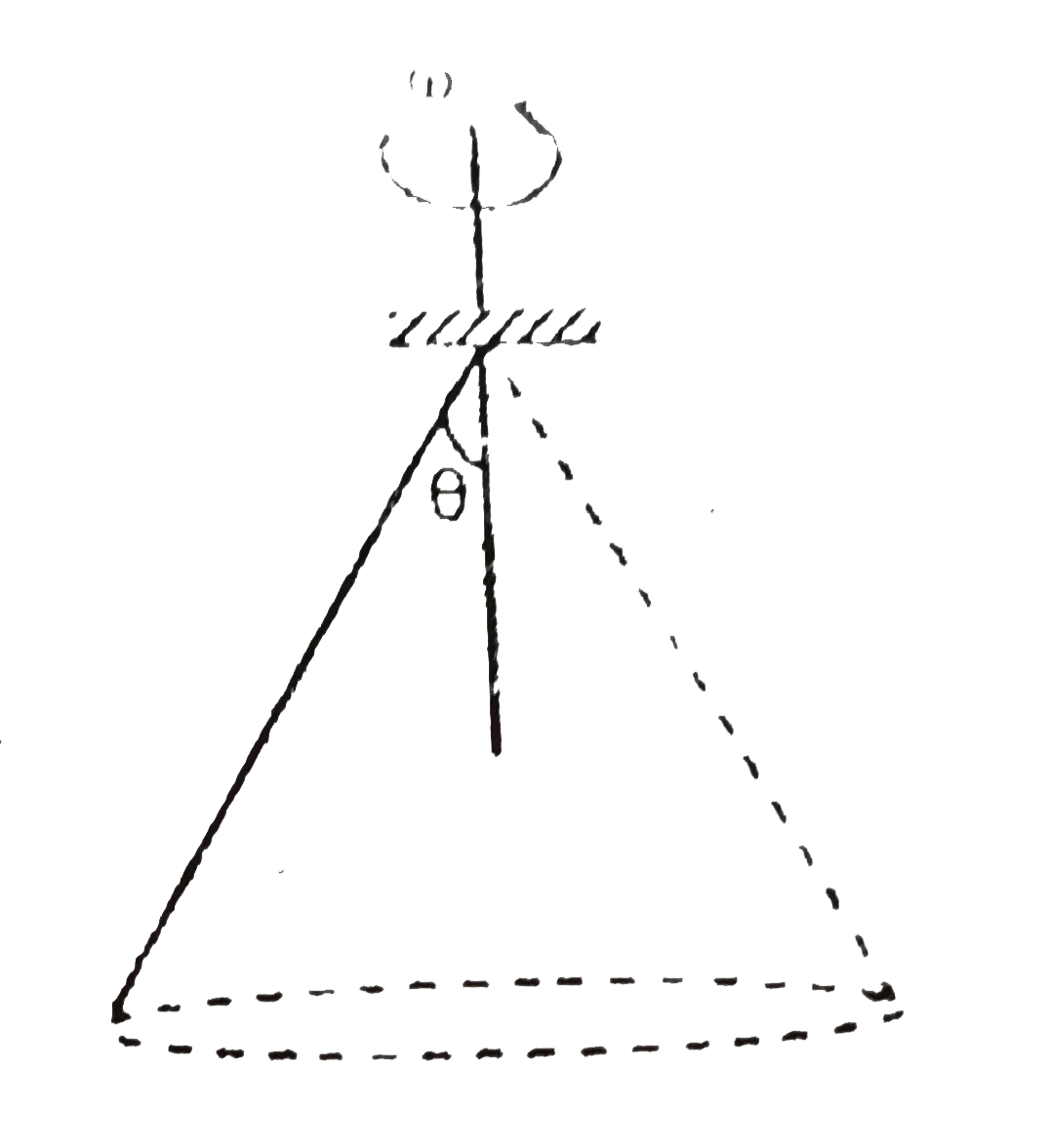
A12Bωl2B34Bωl2CBωl2D2Bωl2A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
In the figure shown a long conductor carries constant current I. A rod PQ of length l is in the plane of the rod.The rod is rotated about point P with constant angular velocity ω as shown in the figure.Find the e.m.f induced in the rod in the position shown.Indicate which points is at high potential.
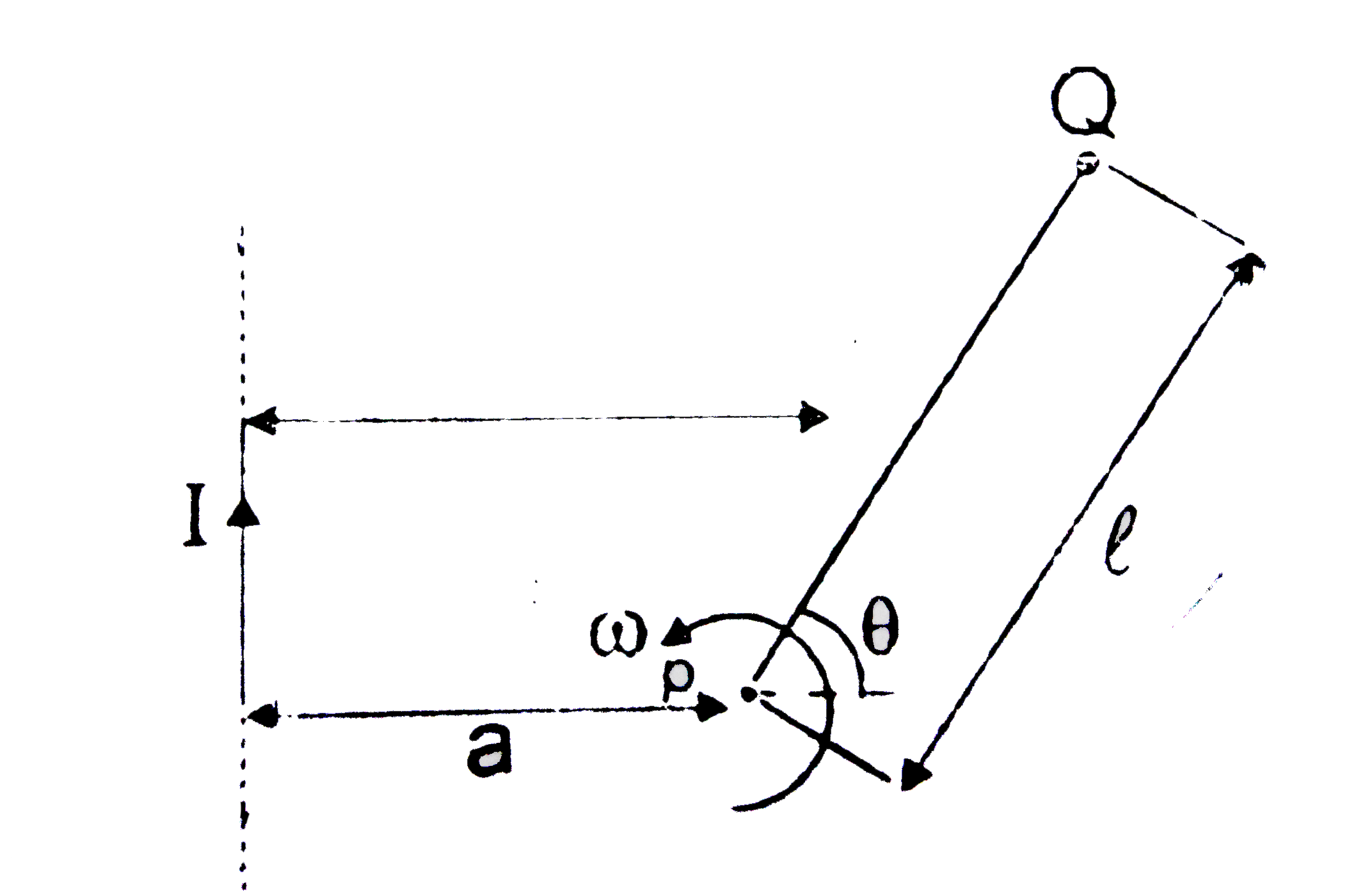
View SolutionIn the figure shown a long conductor carries constant current I. A rod PQ of length l is in the plane of the rod.The rod is rotated about point P with constant angular velocity ω as shown in the figure.Find the e.m.f induced in the rod in the position shown.Indicate which points is at high potential.

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
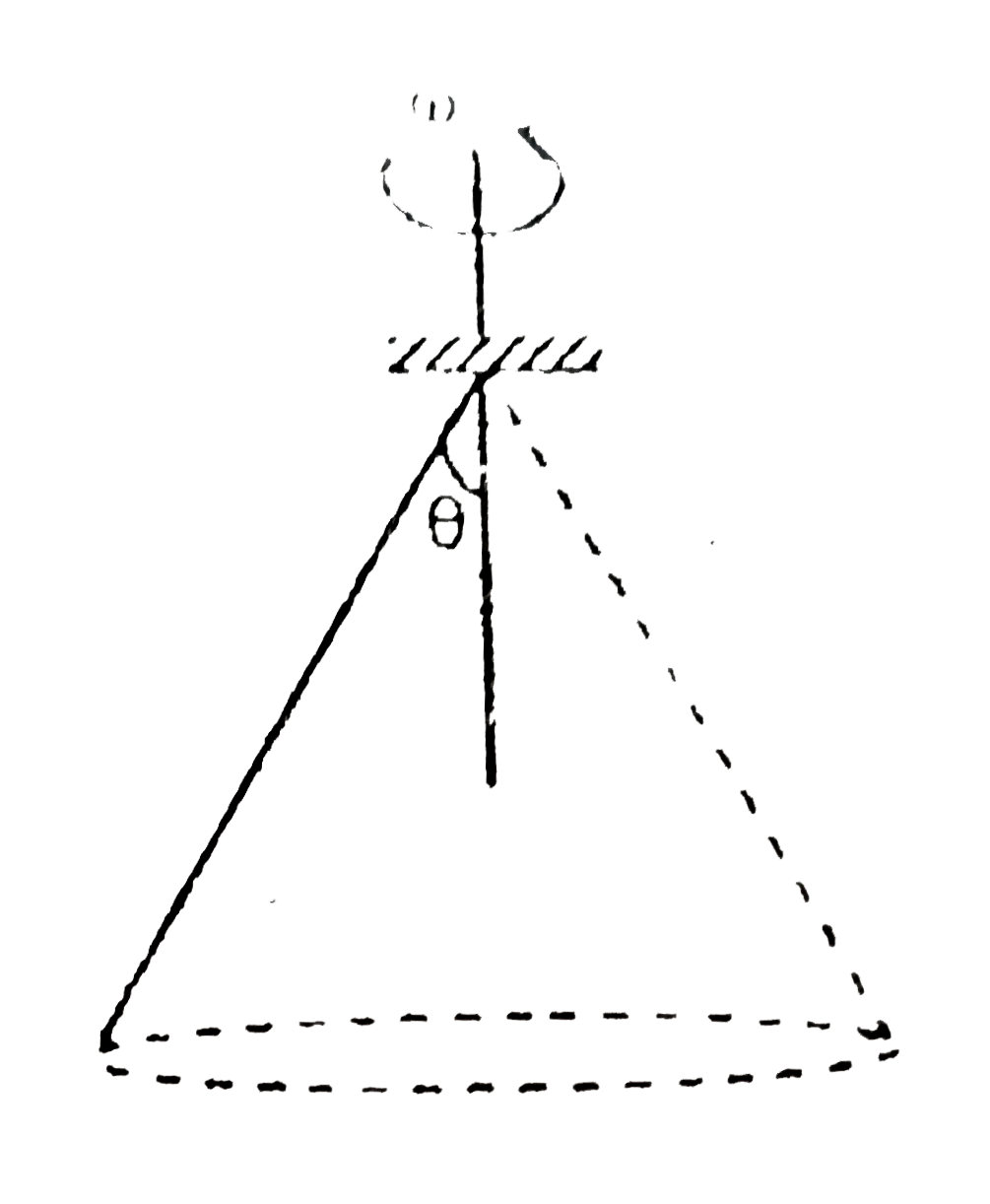
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical

View Solution
