Approximate thickness of oil film to observe interference of light (due to which it looks coloured) is
10 mm
10−3mm
10 cm
1 cm
The correct Answer is:B
To determine the approximate thickness of an oil film required to observe interference of light that results in a colorful appearance, we can follow these steps:
1. Understanding Interference in Thin Films:
- Interference occurs when light waves reflect off the two surfaces of a thin film (in this case, an oil film). The light waves can interfere constructively or destructively, leading to the colorful patterns observed.
2. Path Difference:
- For constructive interference (which produces bright colors), the path difference between the light waves reflecting off the top and bottom surfaces of the film must be an integer multiple of the wavelength of light. The condition for constructive interference is given by:
2t=mλ
where t is the thickness of the film, m is an integer (0, 1, 2,...), and λ is the wavelength of light.
3. Minimum Thickness Calculation:
- To find the minimum thickness t for the first order of interference (m=1), we can rearrange the equation:
t=mλ2
- For visible light, the average wavelength λ is approximately 5000 angstroms (or 5000×10−10 meters).
4. Substituting Values:
- Substituting m=1 and λ=5000 angstroms into the equation gives:
t=1×5000×10−102=2500×10−10 meters
- This can also be expressed in angstroms:
t=2500 angstroms
5. Final Conversion:
- To convert angstroms to millimeters, we know that 1 angstrom=10−10 meters. Therefore:
t=2500×10−10 meters=2.5×10−7 meters=0.25×10−3 millimeters=0.00025 millimeters
6. Conclusion:
- The approximate thickness of the oil film required to observe interference of light is about 2500 angstroms or 0.25 micrometers.
Final Answer:
The approximate thickness of the oil film to observe interference of light is 2500 angstroms.
---
- Interference occurs when light waves reflect off the two surfaces of a thin film (in this case, an oil film). The light waves can interfere constructively or destructively, leading to the colorful patterns observed.
- For constructive interference (which produces bright colors), the path difference between the light waves reflecting off the top and bottom surfaces of the film must be an integer multiple of the wavelength of light. The condition for constructive interference is given by:
2t=mλ
where t is the thickness of the film, m is an integer (0, 1, 2,...), and λ is the wavelength of light.
- To find the minimum thickness t for the first order of interference (m=1), we can rearrange the equation:
t=mλ2
- For visible light, the average wavelength λ is approximately 5000 angstroms (or 5000×10−10 meters).
- Substituting m=1 and λ=5000 angstroms into the equation gives:
t=1×5000×10−102=2500×10−10 meters
- This can also be expressed in angstroms:
t=2500 angstroms
- To convert angstroms to millimeters, we know that 1 angstrom=10−10 meters. Therefore:
t=2500×10−10 meters=2.5×10−7 meters=0.25×10−3 millimeters=0.00025 millimeters
- The approximate thickness of the oil film required to observe interference of light is about 2500 angstroms or 0.25 micrometers.
The approximate thickness of the oil film to observe interference of light is 2500 angstroms.
Similar Questions
Refractive index of a thin soap film of a uniform thickness is 1.38. The smallest thickness of the film that gives an interference maxima in the reflected light when light of wavelength 5520 Å falls at normal incidence is
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.34. Find the smallest thickness of the film that gives in interference maximum in the reflected light when light of wavelength 5360Å fall at normal incidence.
View Solution
Knowledge Check
What is the minimum thickness of thin film required for constructive interference in the reflected light through it ?
(Given, the refractive index of the film =1.5, wavelength of the lilght incident on the film =600 nm.A100 nmB50 nmC200 nmD25 nmA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
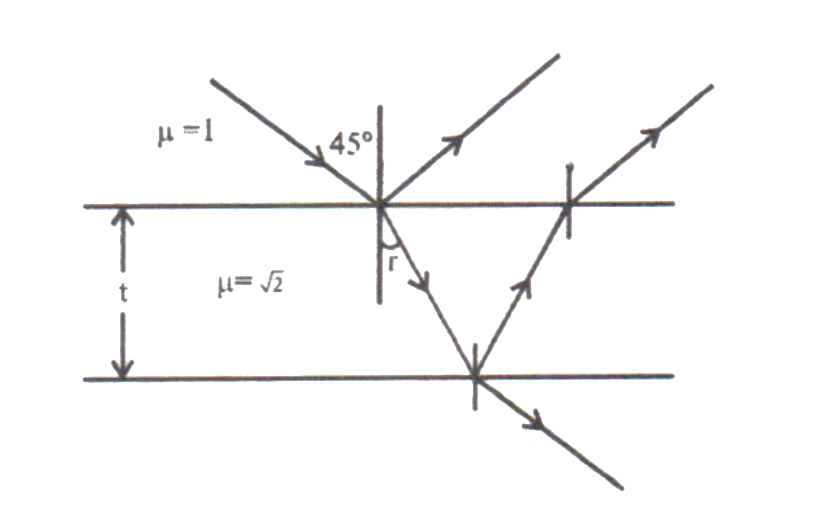 A122 nmB212 nmC173 nmD320 nm
A122 nmB212 nmC173 nmD320 nmWhat is the minimum thickness of thin film required for constructive interference in the reflected light through it ?
(Given, the refractive index of the film =1.5, wavelength of the lilght incident on the film =600 nm.A100nmB150nmC200nmD250nm
Why a thin oil film spread over water appears colourful in light?
View SolutionIf the wavelength of incident light on a soap film is 700 nm then its minimum thickness 10 t nm so that constructive interference in reflected light can be observed. The value of t is ………..[Take refractive index of the film as 43]
View SolutionAn oil film covers the surface of a small pond. The refractive index of the oil is greater than that of water. At one point on the film, the film has the smallest non-zero thickness for which there will be destructive interference in the reflected light when infrared radiation with wavelength 800 nm is incident normal to the film. When this film is viewed at normal incidence at this same point, for what visible wavelengths, if any, will there be constructive interference? (Visible light has wavelengths between 400nm and 700 nm )
View SolutionWhat is the minimum thickness of a soap bubble needed for constructive interference in reflected light, if the light incident on the film is 750 nm? Assume that the refractive index for the film is n=1.33
View SolutionInterference of light is the physcal effect which is produces due to the
View Solution
