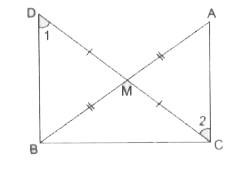
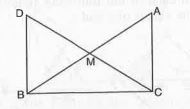
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that
(i) △AMC≅△BMD
(ii) ∠DBC is a right angle.
(iii) △DBC≅△ACB
(iv) CM=12AB
 Solution in Kannada
Solution in Kannada
Step by step video & image solution for In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that (i) triangleAMC ~= triangleBMD (ii) angleDBC is a right angle. (iii) triangleDBC ~= triangleACB (iv) CM = 1/2 AB by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.2
8 Videos
- TRIANGLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.3
5 Videos
- SURFACE AREAS AND VOLUMES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - EXERSICE 13.8
10 Videos
Similar Questions
In an isosceles ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Joint A to O. Show that:
(ii) OB = OC
(ii) AO bisects ∠A
View Solution△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
(i) △ABD≅△ACD
(ii) △ABP≅△ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
View SolutionFind the volume of a sphere whose radius is
(i) 7 cm,
(ii) 0.63m
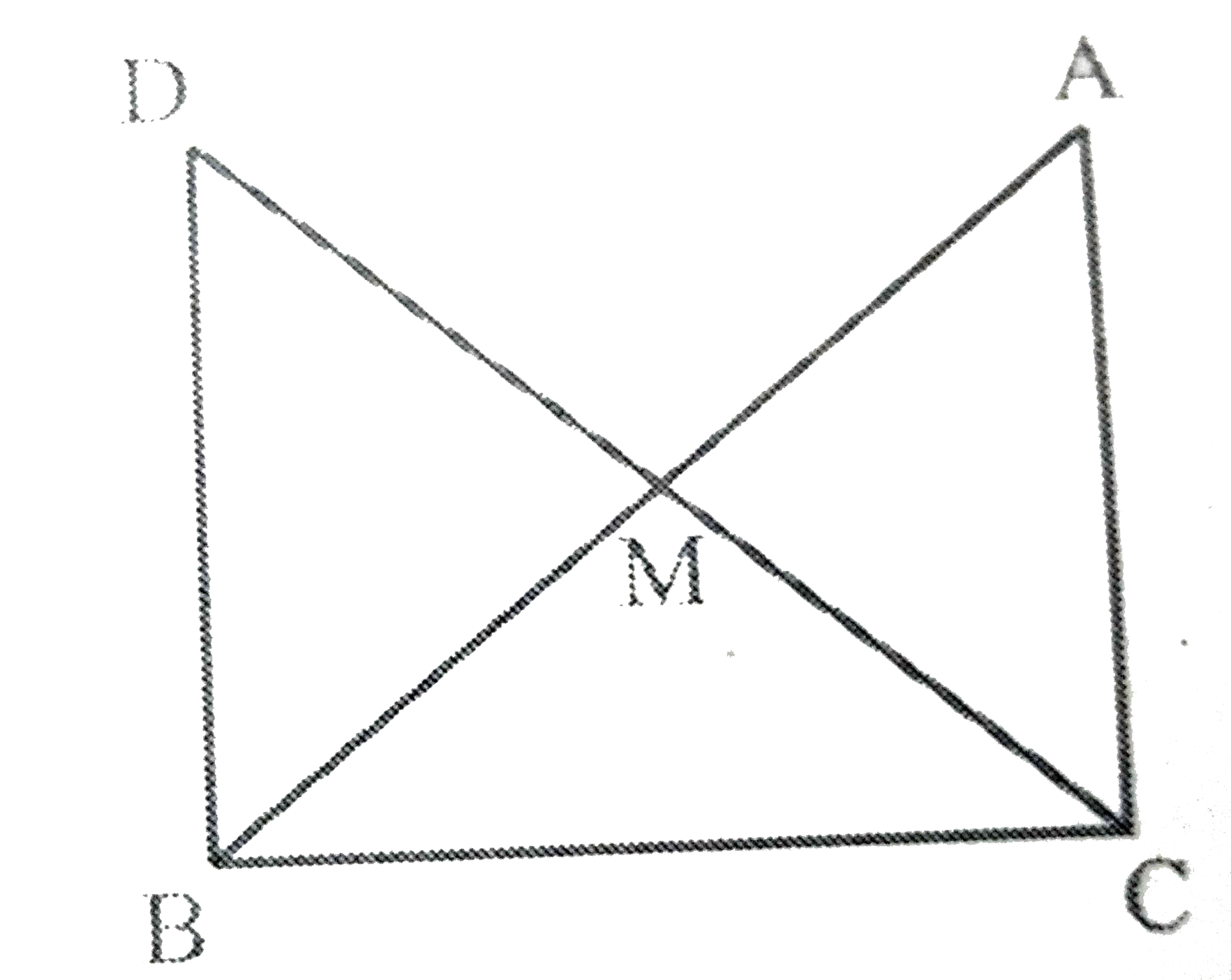
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB
View Solutionएक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है | C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है | बिंदु D को बिंदु B से मिला दिया जाता है (देखिए आकृति) | दर्शाइए कि
∠DBC एक समकोण है
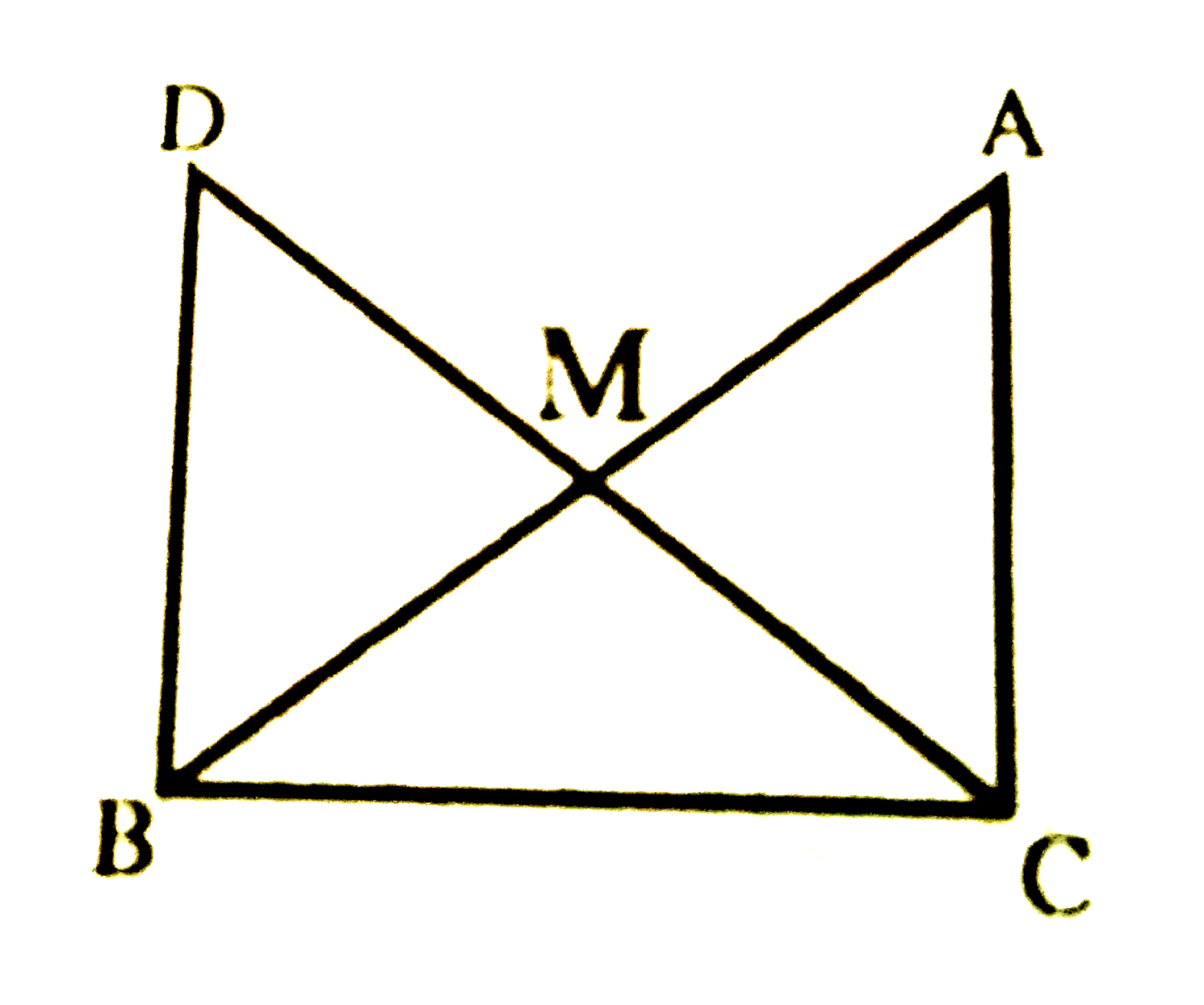
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
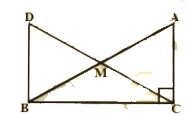
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
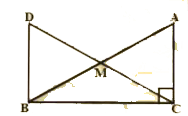
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
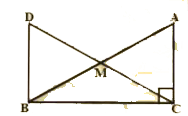
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View SolutionIn right triangle ABC, right angled at C, M is the midpoint of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
(i) △AMC=△BMD
(ii) ∠DBC is a right angle
(iii) △DBC=△ACB
(iv) CM=12 AB
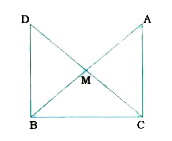
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔAMC≅ΔBMD.
) Show that : ΔAMC≅ΔBMD.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ∠DBC is a right angle.
) Show that : ∠DBC is a right angle.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔDBC≅ΔACB.
) Show that : ΔDBC≅ΔACB.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : CM=12AB.
) Show that : CM=12AB.
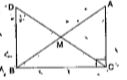
View SolutionIn right triangle ABC, right angle is at 'C'. M s the mid-point of hypotenuse . ABC is joined to M and produced to a point D such that DM = CM. Point D is Joined to point B (see fig.). Show that: CM=12AB
View Solution
