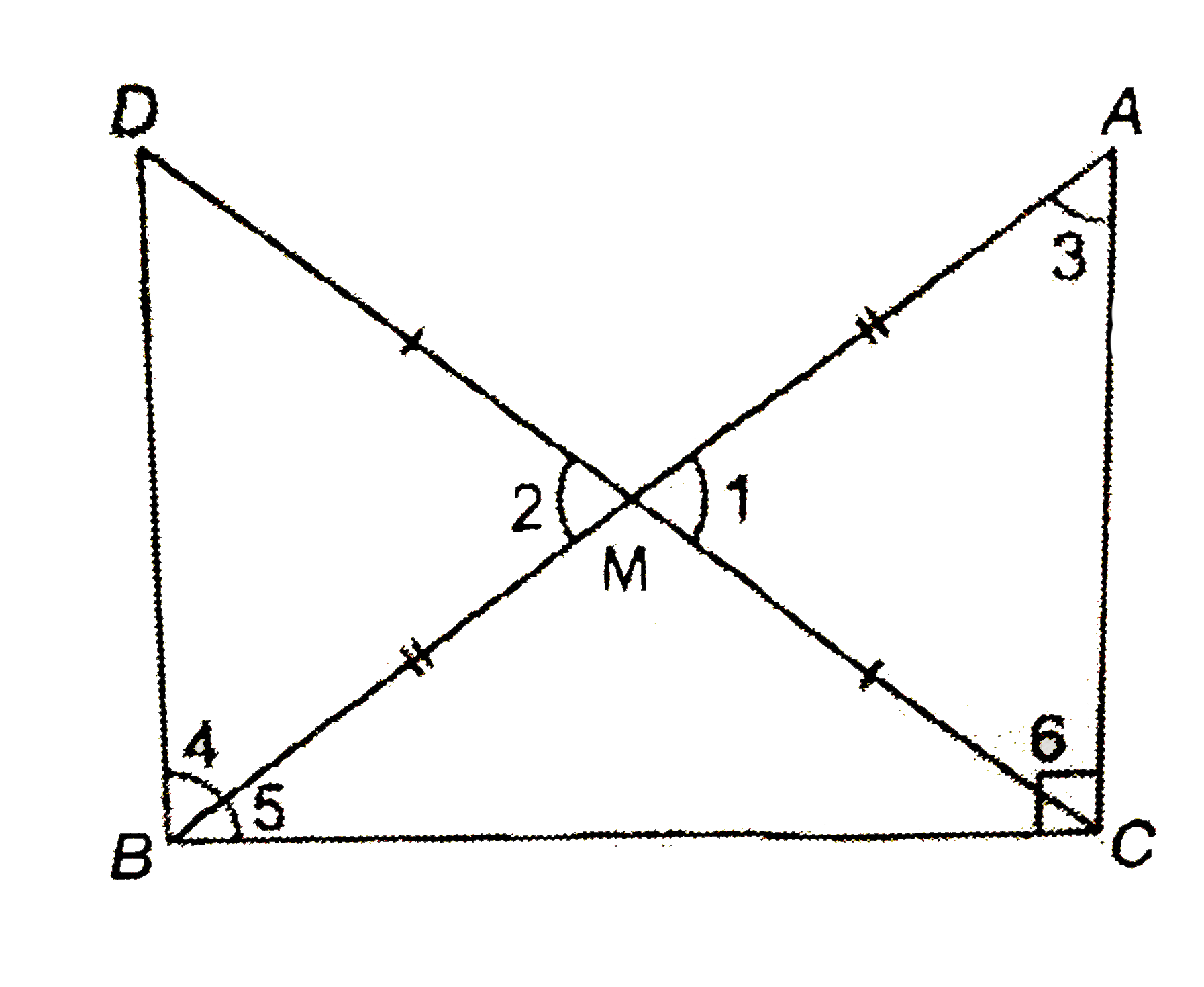
In right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that $D M = C M$ . Point D is joined to point B (see Fig. 7.23). Show that:
(i) $Δ A M C ≅ Δ B M D$
(ii) $∠ D B C$ is a right angle
(iii) $Δ D B C ≅ Δ A C B$
(iv) $C M = \frac{1}{2} A B$
$In right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that D M\ =\ C M. Point D is joined to point B (see Fig. 7.23). Show that: (i) DeltaA M C~=DeltaB M D (ii) /DBC is a right angle (iii) Δ DBC ≅ Δ ACB (iv) CM =1/2 AB$

Video Solution

Text Solution

Verified by Experts

$∠ A M C and ∠ B M D$
AM=BM
MC=MD
$∠ A M C = ∠ B M D$ (VOA)
SAS criteria
$∠ A M C ≅ ∠ B M D$
$∠ C A M = ∠ D B M$
If opposite interiar angles are equal
AC||BD
AC||BD cut by BC
$∠ D B C + ∠ A C B = 180^{0}$
$∠ D B C = 90^{0}$
In $∠ D B C and ∠ A C B$
By SAS criteria
/_DBC cong /_ACB
DC=AB
CM=1/2CD=1/2AB.

Updated on:21/07/2023