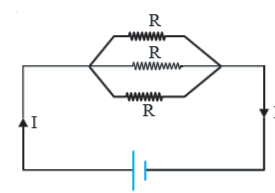
Three equal resistances, each of RΩ are connected as shown in figure. A battery of emf 2 V and internal resistance 0.1Ω is connected across the circuit. Calculate the value of R for which the heat generated in the circuit is maximum?
0.2Ω
0.3Ω
0.4Ω
none of these
The correct Answer is:B
The given network is a parallel combination of three resistances. Combined resistance R/=R/3
Current (I) =ER/3+r
Power (P) = (ER/3+r)2R3=E2R/3[R3−r]2+4Rr3
For maximum power, R3-r=0 or R=3r=0.3Ω
Similar Questions
Three equal resistace, each of R ohm, are connectedd as shown in the figure. A battery of 2V and of internal resistance 0.1 ohm is connected across the circuit. The value of R for which the heat generated in the circuit maximum will be
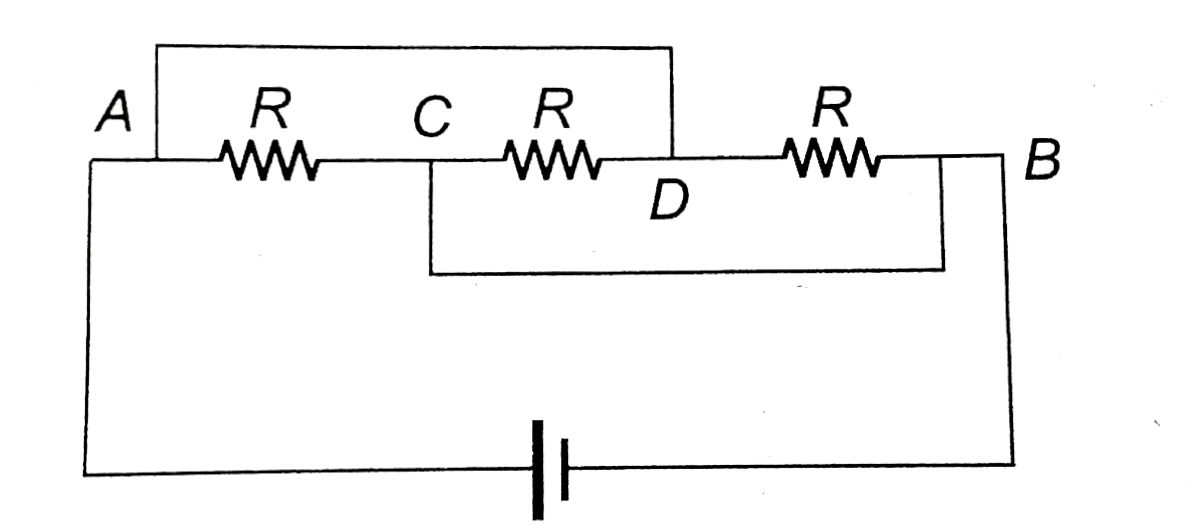
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View Solution
Knowledge Check
Three equal resistace, each of R ohm, are connectedd as shown in the figure. A battery of 2V and of internal resistance 0.1 ohm is connected across the circuit. The value of R for which the heat generated in the circuit maximum will be
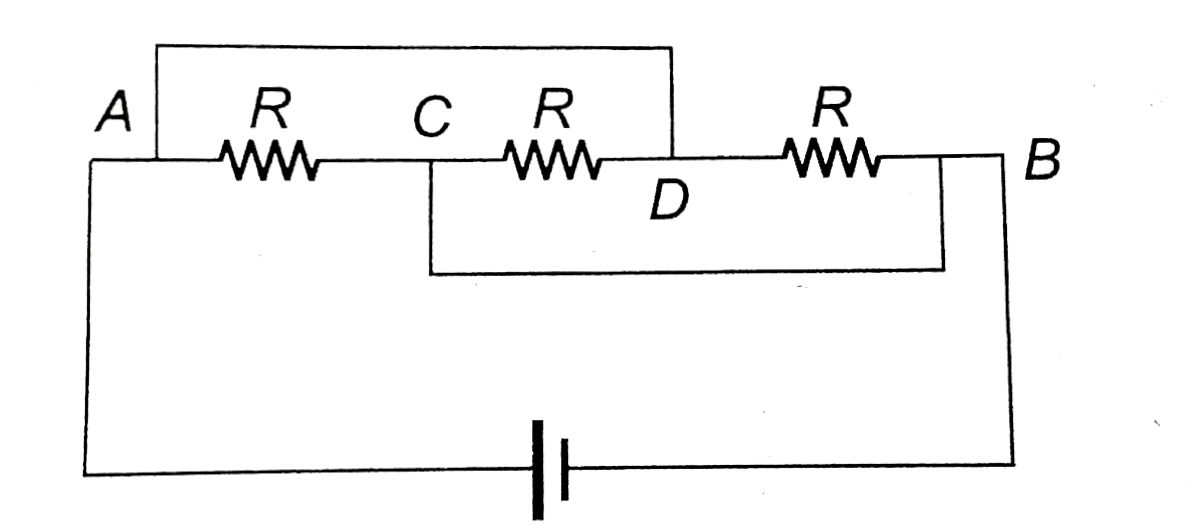 A0.1ΩB0.2ΩC0.3ΩD0.4Ω
A0.1ΩB0.2ΩC0.3ΩD0.4ΩA battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
A2.0ohmB0.25ohmC1.0ohmD0.5ohmA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
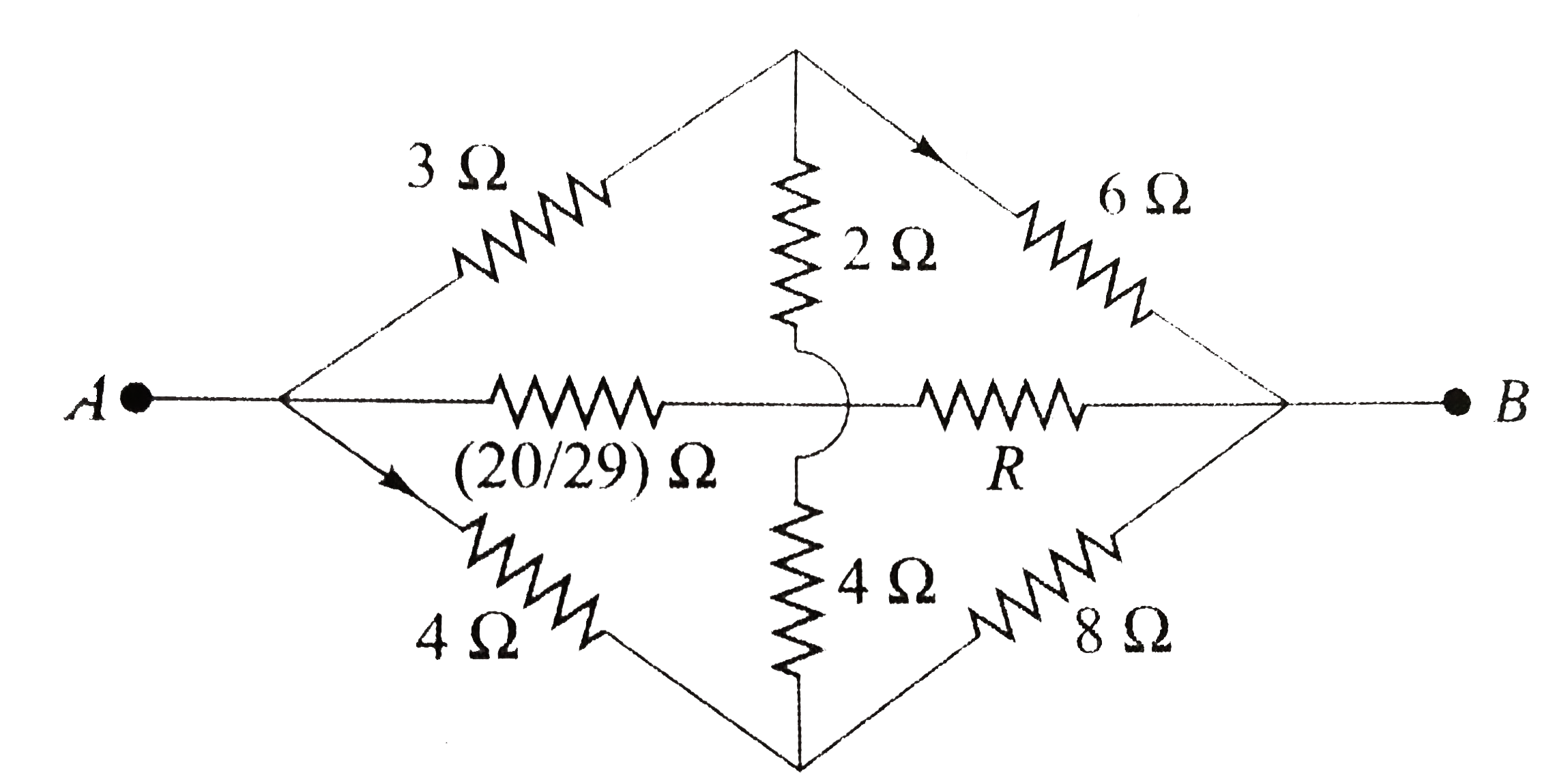 . AThermal power generated in the external circuit will be maximum possible when R=16/25Ω.BMaximum possible thermal power generated in the external circuit is equal to 4 W.CRatio of current through 3Ω to that through 8Ω is independent of R.DNone of above.
. AThermal power generated in the external circuit will be maximum possible when R=16/25Ω.BMaximum possible thermal power generated in the external circuit is equal to 4 W.CRatio of current through 3Ω to that through 8Ω is independent of R.DNone of above.
A battery of e.m.f 10V and internal resistance 3Omega is connected to a resistor.If the current in the circuit is 0.5A,then the resistance of the resistor is
View SolutionSix cells each of e.m.f. 2 V and internal resistance 0.1Ω are connected to three resistances as shown in figure. The reading of a low resistance ammeter A in the circuit is,
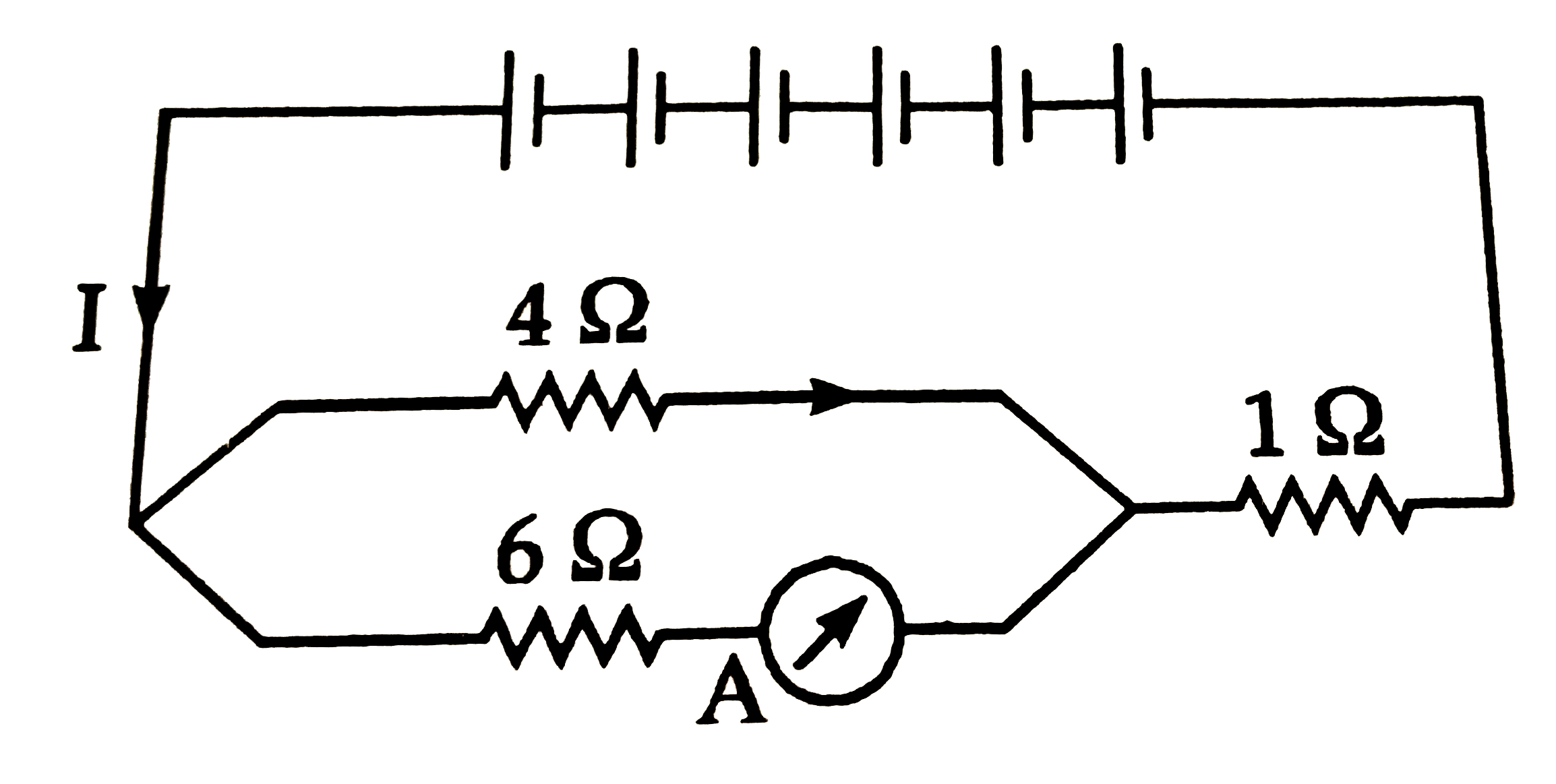
View SolutionThree identical, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionA battery of emf 10 V and internal resistance 3Ωis connected to a resistor. The current in the circuit is 0.5 A . The terminal voltage of the battery when the circuit is closed is
View SolutionA battery of e mf 10 V and internal resistance 3Ω is connected to a resistor as shown in the figure. If the current in the circuit is 0.5 A . then the resistance of the resistor will be
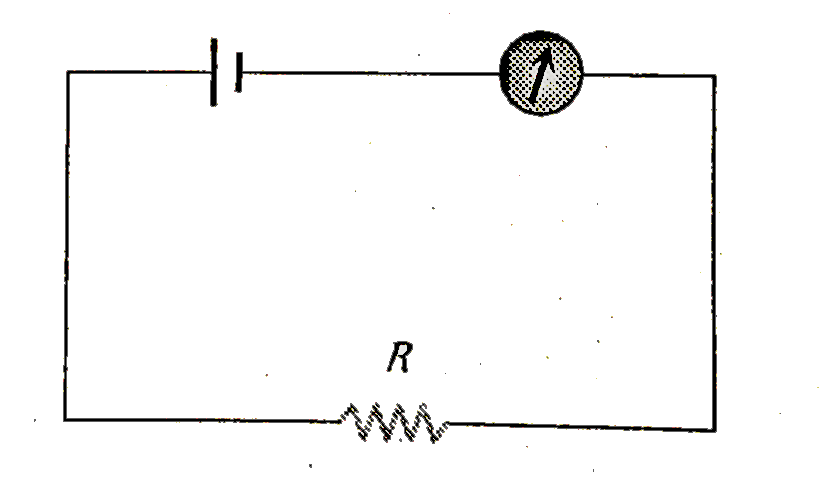
View Solution
