AY and BZ are the diagonals of a parallelogram ABYZ, intersecting at O.ar(ΔBYZ) = ?
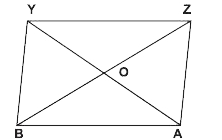
greater than ar(ΔABZ)
is equal to ar(ΔBOA+ΔBOY)
more than ar(ΔBOA+ΔBOY)
less than ar(ΔBOA+ΔBOY)
The correct Answer is:B
Step by step video, text & image solution for AY and BZ are the diagonals of a parallelogram ABYZ, intersecting at O.ar (Delta BYZ) = ? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PART-A (Fill in blanks :)18videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-B5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST3videos
CIRCLES
Similar Questions
Knowledge Check
- Question 1 - Select One
Question Stimulus
The diagonals of a parallelogram ABCD intersect at O. A line through O intersect AB at X and DC at Y. if AB = 10 cm, AD = 9 cm, and OX = 5 cm, then the length of OY isA4 cmB6 cmC5 cmD7 cm - Question 2 - Select One
Question Stimulus
The diagonals of a parallelogram ABCD intersect at O. A line through O intersect AB at X and DC at Y. if AB = 10 cm, AD = 9 cm, and OX = 5 cm, then the length of OY isA1/10B2/10C1/4D5/10
The diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
View SolutionThe diagonals of a parallelogram ABCD intersect at O. If ∠DBC=30∘ and ∠BDC=60∘, then ∠DAB is
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O , a time is drawn to intersect AD at P and BC at Q . Show that PQ divides the parallelogram into two parts of equal area.
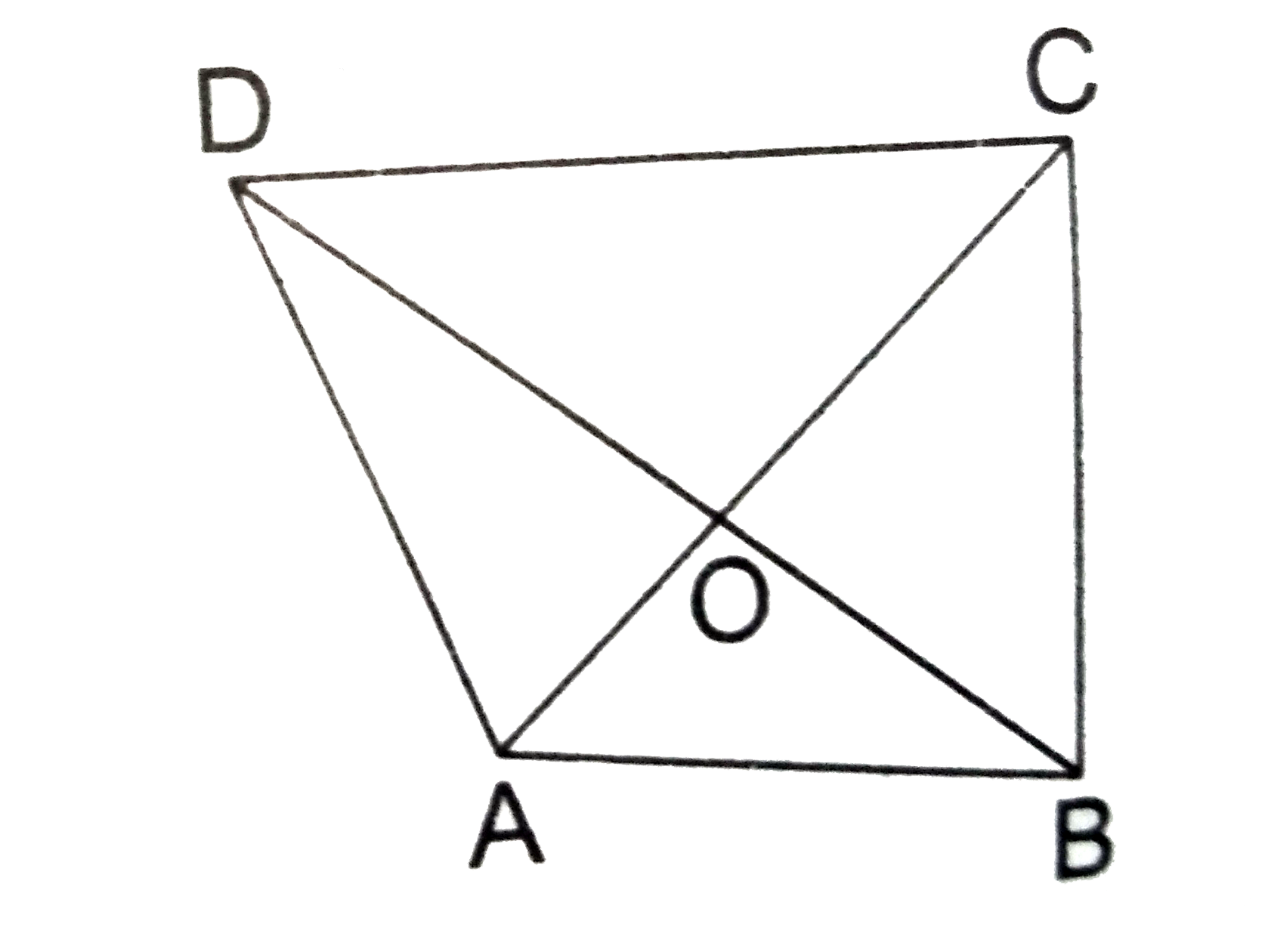
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
 View Solution
View SolutionO' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of ΔAOD= area of ΔAOBView Solution


