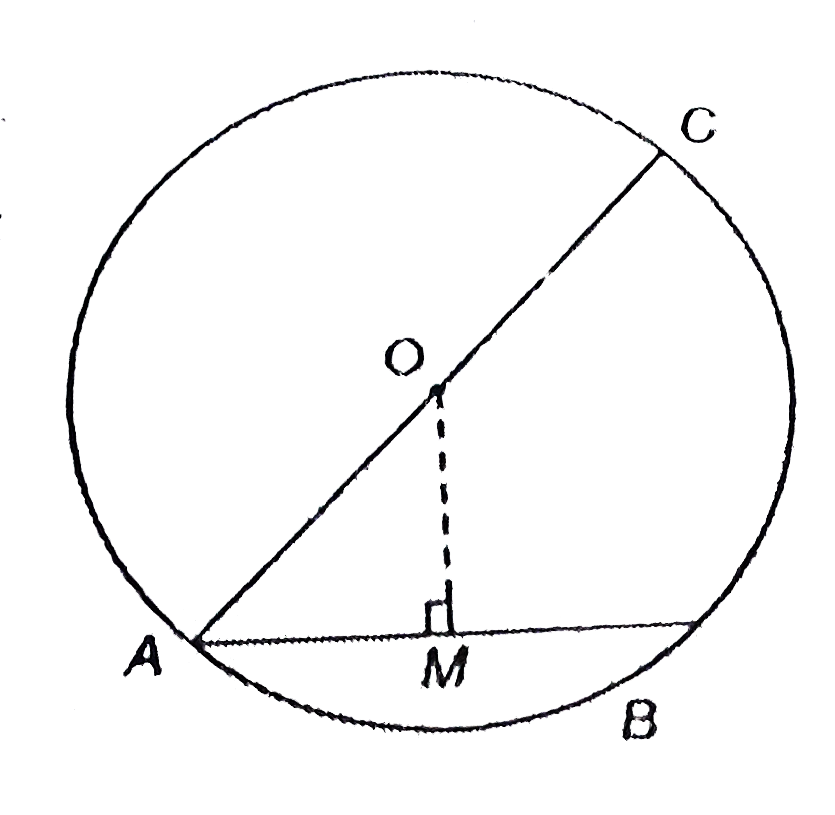
AB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that $4 q^{2} = p^{2} + 3 r^{2}$ .

Video Solution

Answer

Step by step video & image solution for AB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q^(2)=p^(2)+3r^(2). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Topper's Solved these Questions

CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST
3 Videos
CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PART-C
4 Videos
AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PRACTICE TEST
2 Videos
CO-ORDINATE GEOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - PRACTICE TEST
9 Videos

Knowledge Check

There is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
A4.8 cm
B10.8cm
C9.6 cm
Dnone of these